Mesterséges intelligencia a hálózat szélén

Miért most?

A technológia jelenlegi állása szerint képesek vagyunk olyan feladatokra kiképezni a visszacsatolt (mély) neurális hálózatot (DNN), mint az objektum- és az emberi arcfelismerés, a beszédfelismerés, a nyelvfordítás, a játékok (sakk, go, stb.), az autonóm járművezetés, az érzékelők állapotfigyelése, a prediktív gépi karbantartási döntések, az egészségügyi röntgenfelvételek értékelése, stb. Ilyen speciális feladatok esetén a DNN elérheti vagy akár meg is haladhatja az emberi képességeket.

Miért használjon mesterséges intelligenciát a hálózat szélén

Például egy modern épület számos érzékelőt, légkezelő berendezést, felvonót, biztonsági kamerát stb. tartalmaz, amelyek belső hálózatra csatlakoznak. Biztonsági, késleltetési vagy robusztussági okokból helyénvalóbb helyileg, a helyi hálózat szélén mesterséges intelligencia feladatokat futtatni, és csak anonimizált adatokat küldeni a felhőbe, amelyek a globális döntéshozatalhoz szükségesek.

Hardware on the Edge

A DNN hálózat szélére történő telepítéséhez elegendő számítástechnikai teljesítménnyel és alacsony energiafogyasztással rendelkező készülékre van szükség. A jelenlegi technológia állapota alacsony fogyasztású CPU és VPU gyorsítót (x86 CPU SBC + Intel Myriad X VPU) vagy CPU + GPU-t (ARM CPU + Nvidia GPU) kombinál.

A legegyszerűbb módja a DNN elindításának az UP Squared AI Vision X fejlesztői készlet B verziója. A készlet UP Square SBC-n alapul Intel Atom®X7-E3950 processzorral, 8GB RAM, 64GB eMMC, Myriad X MA2485 VPU és 1920x1080 felbontású USB-kamera kézi fókusszal. Előre telepített Ubuntu16.04 (kernel 4.15) és OpenVINO eszközkészlet.

A Toolkit előfordított demo alkalmazásokat tartalmaz a /home/upsquared/build/intel64/Release mappában, és „betanított” modelleket az opt/intel/computer_vision_sdk/deployment_tools/intel_models mappákban. Bármely demo alkalmazás segédeszközének megtekintéséhez futtassa azt a -h opcióval. A demo alkalmazás futtatása előtt javasolt az OpenVINO környezet inicializálása a source /opt/intel/computer_vision_sdk/bin/setupvars.sh parancs által.

Az UP Squared AI Vision X Developer Kit mellett az AAEON kínálatában megtalálhatók még:

1. Myriad X MA2485 VPU-alapú modulok: AI Core X (mPCIe full-size, 1x Myriad X), AI Core XM 2280 (M.2 2280 B+M key, 2x Myriad X), AI Core XP4/ XP8 (PCIE [x4] karta, 4 vagy 8x Myriad X).
2.Nvidia Jetson TX2 modulon alapuló BOXER-8000-es sorozat
3.BOXER-8320AI Core i3-6100U vagy Celeron 3955U processzorral és két AI Core X modul.
4.Boxer-6841M sorozatot Intel Core-I vagy Xeon 6./7. generációs processzoron alapuló alaplappal LGA1151 aljzathoz, és 1x PCIe [x16] vagy 2x PCIe [x8] GPU slot-ok max. 250W-os teljesítménnyel.

Tanulási hardver

Az alábbi táblázat tartalmazza a hardver elméleti csúcsteljesítményét.

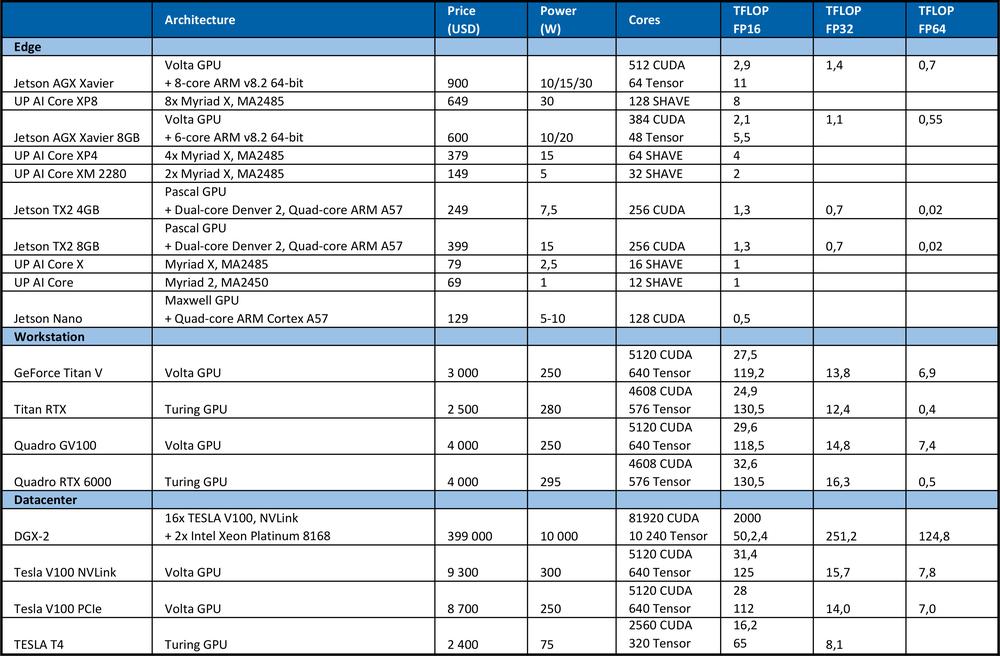
Összehasonlításképpen, a „high end” Intel Xeon Platinum 8180 processzor
●28 magból áll, amelyek magonként 2 AVX-512 és FMA egységet tartalmaznak
●AVX-512 turbófrekvenciával ellátott 2,3 GHz, ha minden mag aktív
●10 000 dollárba kerül.

A kínált elméleti csúcsteljesítmény: magok száma * frekvencia (GHz) * AVX-512 DP FLOPS/Hz * az AVX-512 egységek száma * 2 = 2060.8 GFLOPS dupla pontossággal (DP) → 4,1216 TFLOPS egyszeres pontossággal (32-bit).

Amint az a fenti táblázatból kiderül, a GPU sokkal nagyobb teljesítményt nyújt a neurális hálózatok tanulásához. Meg kell jegyezni, hogy a másodpercenkénti műveletek száma nem az egyetlen paraméter, amely befolyásolja a tanulási teljesítményt. A RAM mérete, a CPU és RAM, GPU és GPU RAM és az egyes GPU-k közötti adatátviteli sebesség szintén befolyásolják a tanulási sebességet.

Szoftver

OpenVINO
Az OpenVINO (open visual inference and neural network) ingyenes szoftver, amely lehetővé teszi az emberi látást utánzó alkalmazások és megoldások gyors telepítését.

Az OpenVINO toolkit:
● CNN-t használ (convolution neural network)
●Képes szétosztani a számításokat az Intel CPU, integrált GPU, Intel FPGA Intel Movidius Neural Compute Stick és az Intel Movidius Myriad VPUs gyorsítók között
●Optimalizált interfészt biztosít az OpenCV, OpenCL és OpenVX számára
●Támogatja a Caffe, TensorFlow, MXNet, ONNX, Kaldi keretrendszereket (framework)

TensorFlow
Az TensorFlow egy nyílt forráskódú könyvtár numerikus számításokhoz és gépi tanuláshoz. Kényelmes front-end API-t biztosít a Python programozási nyelv alkalmazásainak létrehozásához. Ugyanakkor maga a TensorFlow által generált alkalmazás is optimalizált C ++ kódokká alakul, amely számos platformon futtatható, mint például CPU-k, GPU-k, helyi számítógépek, felhőcsoportok, beágyazott rendszerek a hálózat szélén, és hasonlók.

Egyéb hasznos szoftverek
Jupyter Lab / Notebook
https://jupyter.org/index.html
https://github.com/jupyter/jupyter/wiki/Jupyter-kernels
https://jupyterlab.readthedocs.io/en/stable
Keras
Pandas 
MatplotLib 
Numpy 

Hogyan működik?

Egyszerűsített neuronmodell
Egyszerű neuronmodell – a perceptront első ízben Warren McCulloch és Walter Pitts írták le, és még mindig referenciaszintként szolgál a neurális hálózatok terén.

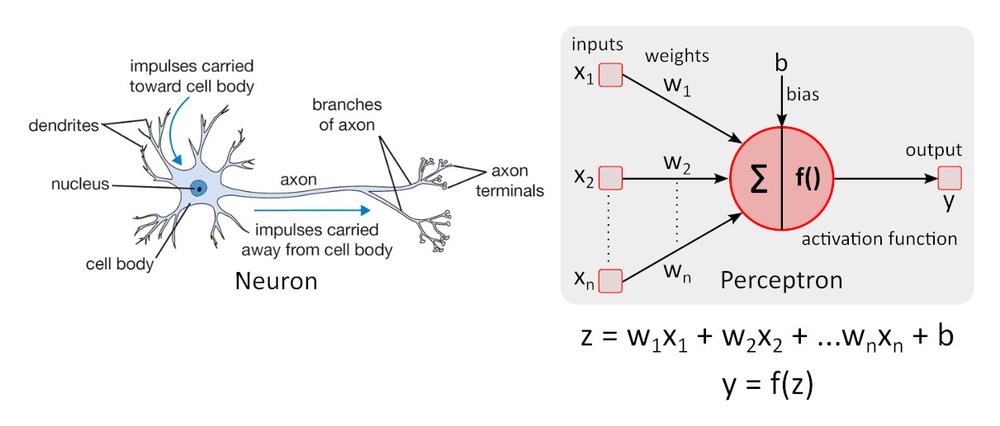
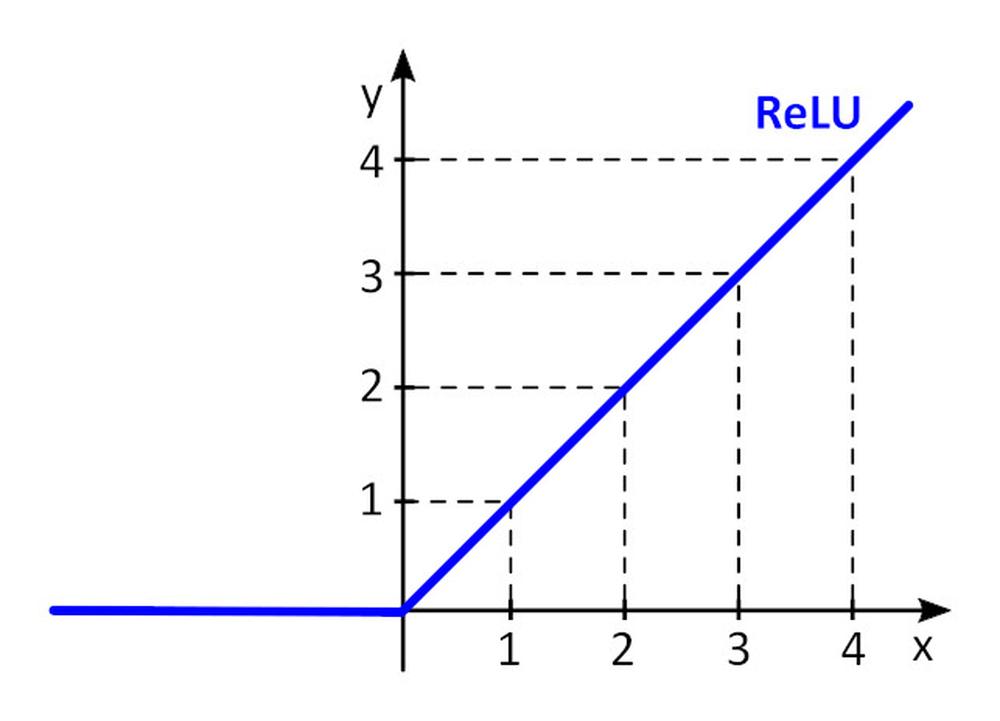
Az f () aktivációs függvény nem-linearitást ad a perceptonba. Nem-lineáris aktivációs függvény nélkül a perceptronokból álló neurális hálózat (NN) – függetlenül attól, hogy hány rétegből áll – egyrétegű perceptronként viselkedne, mert az egyes rétegek összegzése további lineáris függvényt eredményezne. A leggyakrabban használt aktivációs funkció a ReLU (rectified linear unit).

y = f(x) = max (0, x), ha x < = 0, y = 0, vagy x ≥ 0, y=x

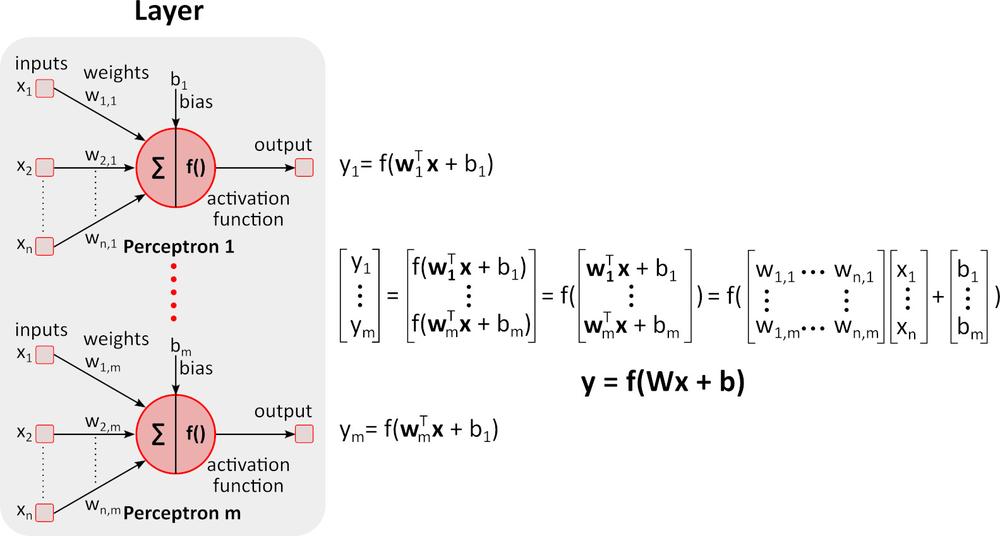
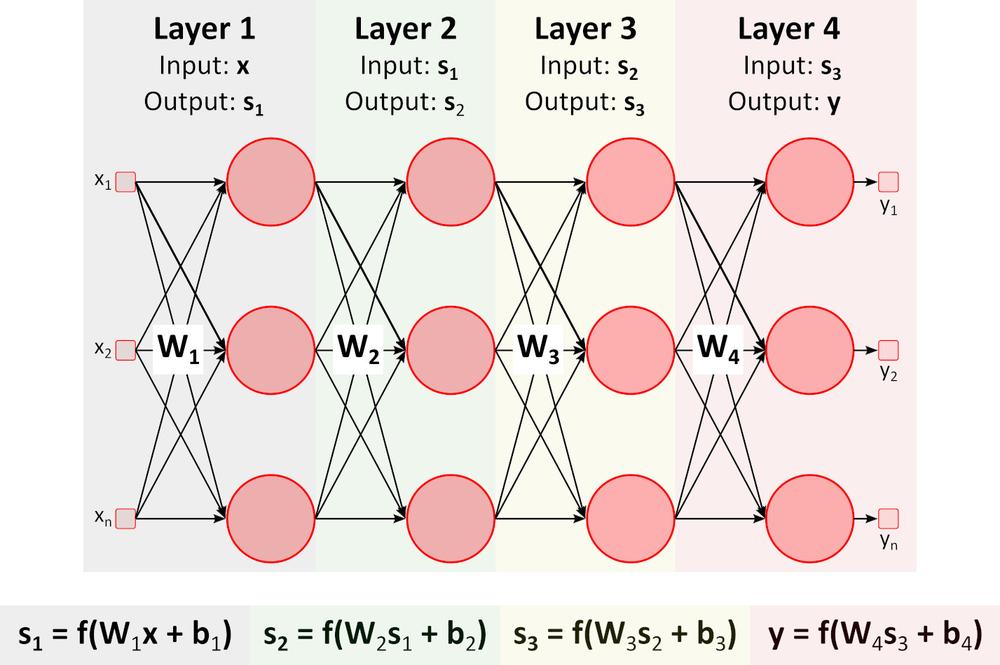
Tanulás (Backward pass)

Tanulás (Spätný prechod)

PTegyük fel, hogy meg szeretnénk tanítani a DNN-nek, hogy felismerje egy képen egy narancsot, banánt, almát és málnát, tehát az objektumosztályokat.

Nagyszámú fényképet készítünk a fent említett gyümölcsökről, és tanuló és ellenőrző csoportra osztjuk őket. A tanuló szett fényképeket és helyes válaszokat tartalmaz. A DNN 4 kimenettel rendelkezik. Az első kimenet pontot (valószínűséget) ad, hogy a képen látható gyümölcs narancs, a második a banán, stb.

1. Beállítjuk a kezdeti értékeket valamennyi súlyhoz (weight) és torzításhoz (bias) b_i. Ezek általában véletlenszerű értékek.

2.Lefuttatjuk az első képet a DNN-en. A hálózat valamennyi kimeneten pontszámot (valószínűséget) ad.

3.Tegyük fel, hogy az első kép narancsot ábrázol. A hálózati kimenetek ezáltal a következőképpen alakulnak: y = (narancs, banán, alma, málna) = (0,5, 0,1, 0,3, 0,1). A hálózat szerint annak a valószínűsége, hogy az első képen narancs látható 0,5.

4.Meghatározzuk a veszteség (hiba) függvényt, amely számszerűsíti a becsült pontszám és a tényleges pontszám közötti egyezést. A leggyakoribb függvény: E = 0.5*sum (e_j)^2, ahol e_j = y_j-y_real_j, a j pedig a tanuló szettben található képek száma. E_1_narancs = 0.5*(0.5-1)^2=0.125, E_1_banán =.0.5*(0.1-0)^2 = 0.005 E_1_alma = 0.5*(0.3-0)^2 = 0.045, E_1_málna = 0.5*(0.1-0)^2 = 0.005 E_1 = (0,125 0,005 0,045 0,005)

5.Lefuttatjuk a tanuló készlet maradék képeit is a DNN-en, és kiszámítjuk a teljes készlet veszteségfüggvényét, az E-t (E_narancs E_ banán E_alma E_málna)

6.Ahhoz, hogy meghatározzuk a következő átáramoltatásra (epoch) vonatkozó valamennyi súlyt (w_i) és torzítást (b_i), ismernünk kell minden egyes w_i és b_i paraméter hatását az egyes osztályok veszteségfüggvényére. Ha egy paraméter értékének növelése növeli a veszteségfüggvény értékét, csökkentenünk kell ezt a paramétert és fordítva. De hogyan számoljuk ki a paraméterértékek növelését vagy csökkentését?

Lássunk egy egyszerű példát.

Adott három pont (x, y): (1, 3), (2.5, 2), (3.5, 5). Egy olyan egyenest keresünk y = w.x + b, ahol a veszteségfüggvény minimális lesz: E = 0.5*sum (e_j)^2, ahol _j = y_j – y_real_j, és j=1, 2, 3. A feladat leegyszerűsítése érdekében, tegyük fel, hogy w = 1,2, és csak a b értéket keressük. Kezdeti értékként válasszuk a b = 0 –t.

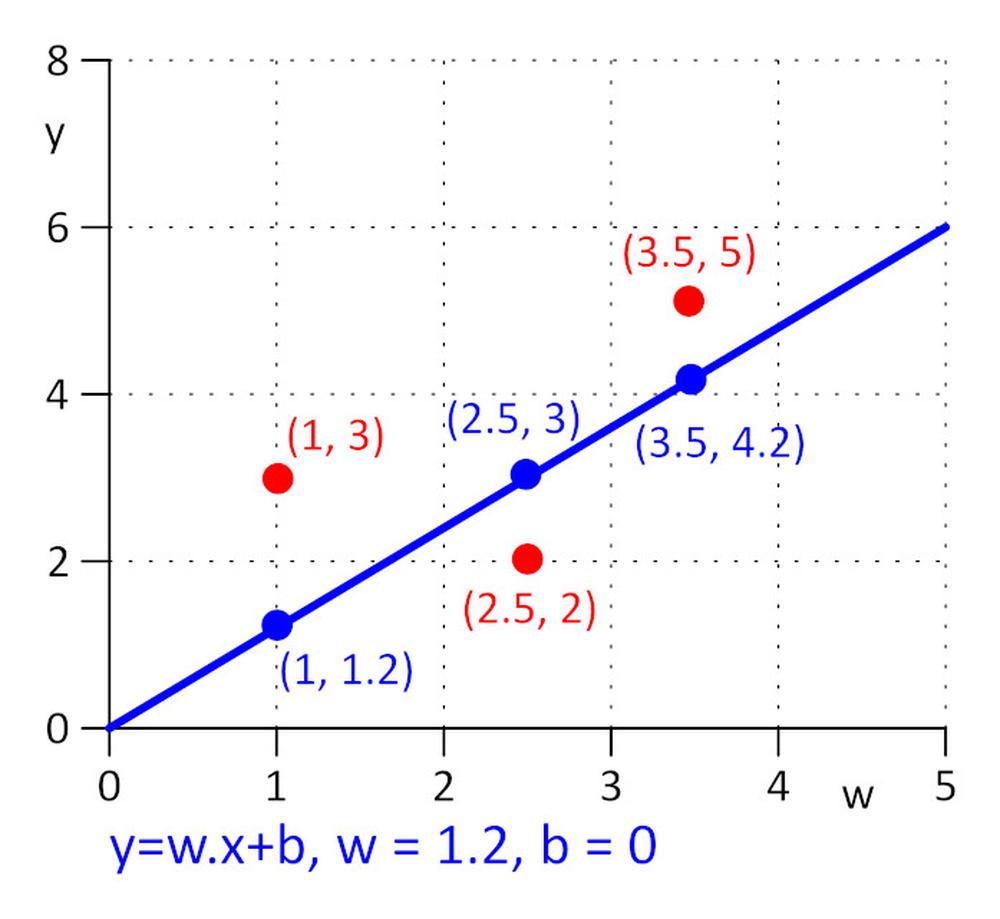
Számítsuk ki a veszteségfüggvényt: E = 0,5*sum ( e_j)^2 = 0,5*(e_1^2 + e_2^2 + e_3^2), e_1=1,2*1 + b -3, e_2 = 1,2*2,5 + b – 2, e_3 = 1,2*3,5 + b – 5.

A veszteségfüggvény egyszerű, az E minimum értékét az alábbi képlet kiszámításával kapjuk meg: ∂E/∂b = 0. Ez egy összetett függvény, a ∂E/∂b kiszámításához a kompozit függvény deriválására vonatkozó szabályt használjuk.

∂E/∂b=0.5*((∂E/∂e_1)*(∂e_1/∂b) + (∂E/∂e_2)*(∂e_2/∂b) + (∂E/∂e_3)*(∂e_3/∂b)) = 0.5*(2*e_1*1 + 2*e_2*1 + 2*e_3*1) = (1.2*1 + b – 3) + (1.2*2.5 + b – 2) + (1.2*3.5 + b – 5) = 0 => b = 0.53333.

A gyakorlatban, ahol a w_i és b_i paraméterek száma elérheti a milliót vagy többet, nem célszerű közvetlenül a ∂E/∂b_i=0 és ∂E/∂b_i= 0 egyenleteket használni, helyette iteratív algoritmus ajánlott.

Kezdetnek lássuk a b = 0 esetet. A következő érték b_1 = b_0 – η*∂E/∂b, ahol η a tanulási sebesség (hiperparaméter), a -η*∂E/∂b pedig a lépés mérete. A tanulásst megállítjuk, ha a mérete eléri a megadott határértéket, a gyakorlatban ez 0,001 vagy kevesebb. Az η = 0,3 esetében b_1 = 0,48, b_2 = 0,528, b_3 = 0,5328 b_4 = 0,53328 és b_5 = 0,5533328. 5 iteráció után a lépés mérete 4,8e-5-re csökkent, és itt megszakítjuk a tanulást. Az algoritmussal kapott b érték gyakorlatilag megegyezik az ∂E / ∂b = 0 egyenlet megoldásával kapott értékkel.

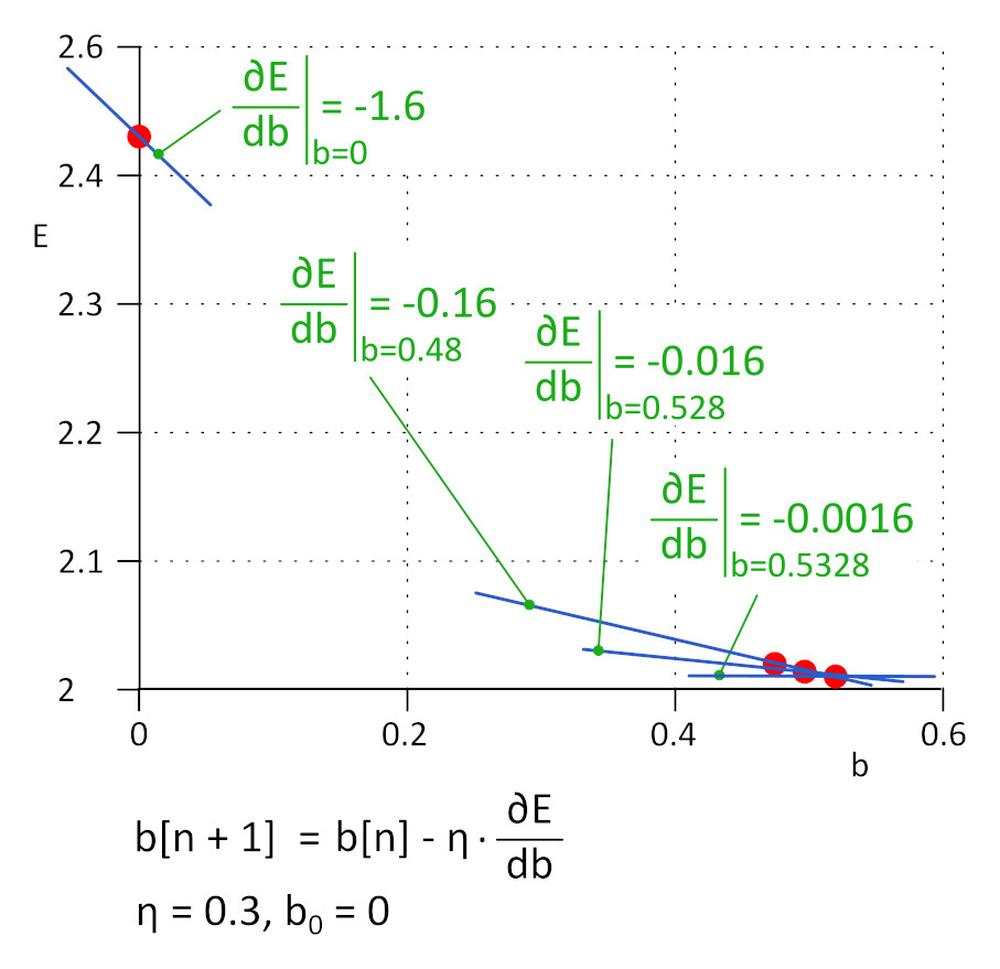
Ezt a módszert gradiens módszernek nevezik.

A tanulási arány fontos hiperparaméter. Ha túl kicsi, sok lépést kell tennie a minimális veszteségfüggvény megtalálásához; ha magas, az algoritmus sikertelen lehet. A gyakorlatban az algoritmus javított változatai, mint például az Adam, használatosak.

7.Ismételjük az 5. és 6. lépést mindaddig, amíg a veszteségfüggvény értéke a kívánt értékre nem csökken.

8.Elvégeztük az érvényesítést a képzett DNN-en keresztül, és értékeljük a pontosságot.

Napjainkban a DNN-tanulás magas kísérleti szakaszban van. Számos DNN architektúra ismert, ezek mindegyike jól illeszkedik bizonyos feladatokhoz. Minden DNN architektúrának van saját hiperparamétere, amely befolyásolja a viselkedését. Vértezze fel magát türelemmel, és az eredmény nem marad el.

További AAEON termékkel kapcsolatos kérdésével, forduljon hozzánk bizalommal az aaeon@soselectronic.hu címen.