Proč nyní?

Při současném stavu technologie dokážeme natrénovat hlubokou neuronovou síť (DNN) pro specifické úlohy jako je detekce a rozpoznávání objektů a lidské tváře, rozpoznávání řeči, překlad jazyka, hry (šachy, go atd.), autonomní řízení vozidla, sledování stavu senzorů a rozhodování o prediktivní údržbě strojů, vyhodnocování rentgenových snímků ve zdravotnictví atd. Pro takové specializované úkoly může DNN dosáhnout nebo dokonce převýšit lidské schopnosti.
Proč používat umělou inteligenci na okraji sítě
Například moderní budova obsahuje množství snímačů, vzduchotechnických zařízení, výtahů, bezpečnostních kamer atd. Z důvodů bezpečnosti, latence nebo robustnosti je vhodnější, aby úkoly umělé inteligence běžely lokálně, na okraji lokální sítě, a do cloudu budeme posílat pouze anonymizované údaje, které jsou potřebné k přijímání globálních rozhodnutí.
Hardware na okraji sítě
Pro nasazení DNN na okraji sítě potřebujeme zařízení s dostatečným výpočetním výkonem, současně s nízkou spotřebou energie. Momentální stav technologií nabízí kombinaci CPU s nízkým příkonem a VPU akcelerátorem (x86 CPU SBC+ Intel Myriad X VPU) nebo CPU + GPU (ARM CPU + Nvidia GPU)
Nejjednodušším způsobem jak začít s DNN je použít UP Squared AI Vision X Developer Kit verzi B. Kit je založen na procesoru UP Square SBC s procesorem Intel Atom®X7-E3950, 8GB RAM, 64GB eMMC, Myriad X MA2485 VPU a USB kameru s rozlišením 1920 x 1080 s manuálním ostřením. Na kitu je předinstalována distribuce Ubuntu 16.04 (kernel 4.15) a OpenVINO toolkit 2018 R5.
Toolkit obsahuje překompilované demo aplikace ve složce /home/upsquared/build/intel64/Release a přetrénované modely ve složce /opt/intel/computer_vision_sdk/deployment_tools/intel_models. Chcete-li zobrazit pomůcky pro jakoukoliv demo aplikaci, spusťte ji v terminálu s volbou –h. Před spuštěním aplikace je nutné inicializovat prostředí OpenVINO příkazem source /opt/intel/computer_vision_sdk/bin/setupvars.sh.
Mimo UP Squared AI Vision X Developer Kitu nabízí AAEON:
1. Moduly založené na Myriad X MA2485 VPU: AI Core X (mPCIe full-size, 1x Myriad X), AI Core XM 2280 (M.2 2280 B+M key, 2x Myriad X), AI Core XP4/ XP8 (PCIE [x4] karta, 4 nebo 8x Myriad X).
2. Sérii BOXER-8000 založenou na modulu Nvidia Jetson TX2.
3. BOXER-8320AI s procesorem Core i3-6100U nebo Celeron 3955U a dvěma AI Core X moduly.
4. Sérii Boxer-6841M se základní deskou pro procesory Intel Core-I nebo Xeon 6./ 7. generace pro patici LGA1151 a 1x PCIe [x16] nebo 2x PCIe [x8] sloty pro GPU s max. příkonem 250W.
Hardware pro učení
Pro trénování DNN potřebujeme vysoký výpočetní výkon. Například na soutěži ImageNet v roce 2012 použil vítězný tým konvoluční neuronovou síť AlexNet. Pro učení bylo potřebných 1.4 ExaFLOP = 1,4e6 TFLOP operací. Učení zabralo 5 až 6 dní na dvou Nvidia GTX580 GPU, kde každá měla výpočetní výkon 1,5 TFLOPS.Následující tabulka shrnuje teoretický špičkový výkon hardwaru.
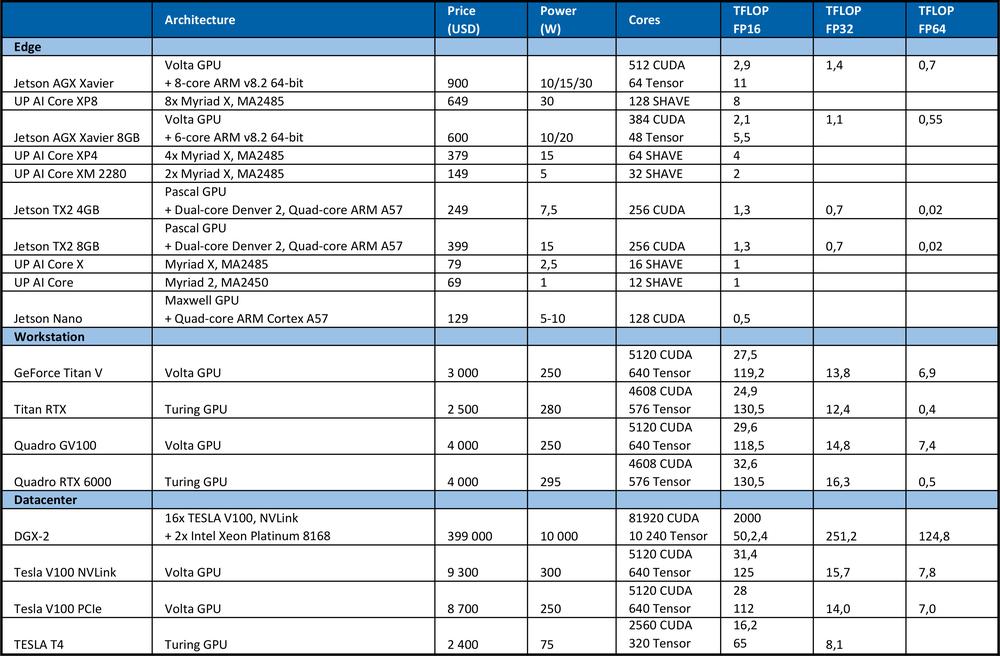
Pro porovnání, špičkový procesor Intel Xeon Platinum 8180
●má 28 jader se dvěma AVX-512 & FMA jednotkami na jádro
●AVX-512 turbo frekvenci 2,3GHz, pokud jsou aktivní všechna jádra
●stojí 10 000 USD.
Nabízí teoretický špičkový výkon: počet jader * frekvence v GHz * AVX-512 DP FLOPS/Hz * počet AVX-512 jednotek * 2 = 2060.8 GFLOPS v dvojnásobné přesnosti (DP) → 4,1216 TFLOPS v jednoduché přesnosti (32bit).
Jak můžete vidět z tabulky výše, GPU poskytuje mnohem více výkonu pro učení neuronových sítí. Je třeba poznamenat, že počet operací za sekundu není jediným parametrem, který ovlivňuje rychlost učení. Faktory jako velikost RAM, rychlost přenosu dat mezi CPU a RAM, GPU a GPU RAM a mezi jednotlivými GPU rovněž ovlivňuje rychlost učení.
Software

OpenVINO
OpenVINO (open visual inference and neural network) je bezplatný software, který umožňuje rychlé nasazení aplikací a řešení, která napodobují lidské vidění.
OpenVINO toolkit:
● Používá CNN (convolution neural network)
●Dokáže rozdělit výpočty mezi Intel CPU, integrovanou GPU, Intel FPGA, Intel Movidius Neural Compute Stick a akcelerátory s Intel Movidius Myriad VPUs
●Poskytuje optimalizované rozhraní pro OpenCV, OpenCL a OpenVX
●Podporuje Caffe, TensorFlow, MXNet, ONNX, Kaldi frameworky
TensorFlow
TensorFlow je open source knihovna pro numerické výpočty a strojové učení. Poskytuje pohodlné front-end API pro vytváření aplikací v programovacím jazyce Python, samotná aplikace vygenerovaná knihovnou TensorFlow je ale překonvertována do optimalizovaného kódu v C ++, která po zkompilování může běžet na různých platformách, jako jsou CPU, GPU, lokální počítač, clusteru v cloudu, embedded zařízeních na okraji sítě a podobně.
Ostatní užitečný software
Jupyter Lab / Notebook
https://jupyter.org/index.html
https://github.com/jupyter/jupyter/wiki/Jupyter-kernels
https://jupyterlab.readthedocs.io/en/stable
Keras
Pandas
MatplotLib
Numpy
Jak to funguje?
Zjednodušený model neuronu
Zjednodušený model neuronu – perceptron byl poprvé popsán Warrenem McCullochem a Walterem Pittsem, platí stále za referenční normu v oblasti neuronových sítí.
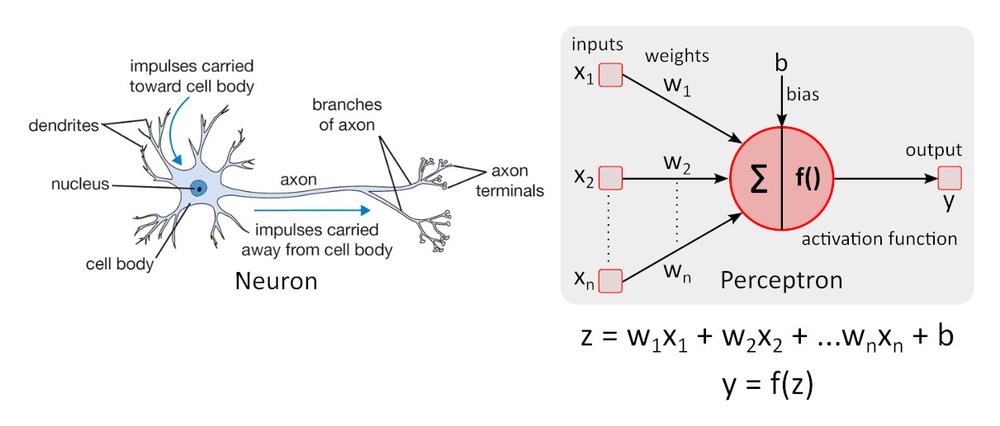
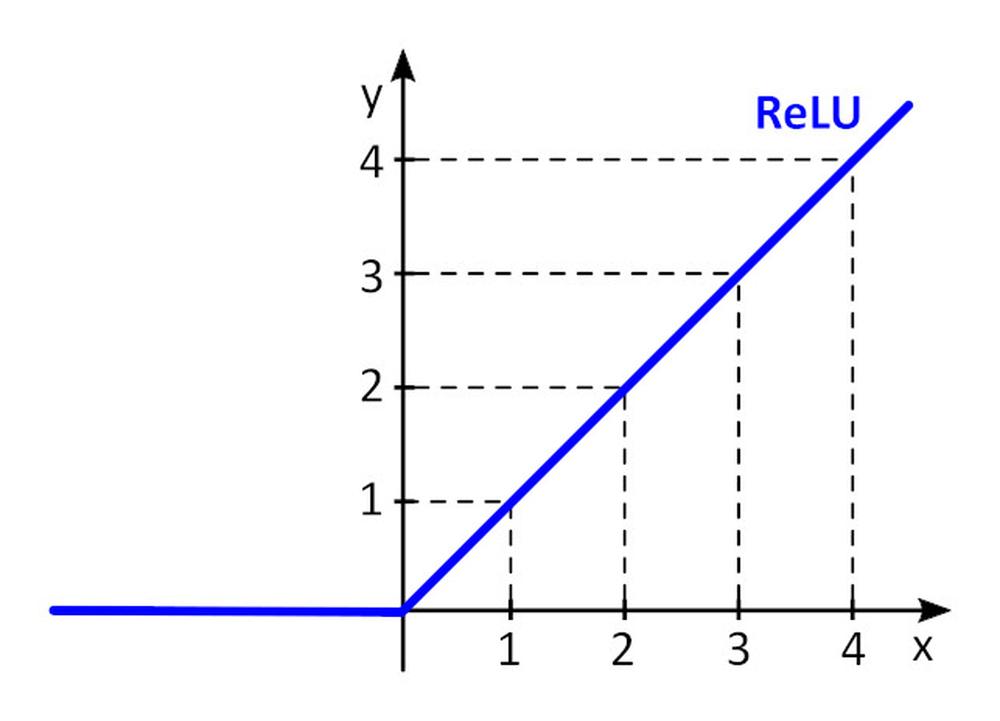
Aktivační funkce f () přidává do perceptronu nelinearitu. Bez nelineární aktivační funkce v neuronové síti (NN) složené z perceptronů, bez ohledu na to, kolik by měla vrstev, by se chovala jako jednovrstvý perceptron, protože sčítání těchto vrstev by nám poskytlo jen další lineární funkci. Nejčastěji používanou aktivační funkcí je ReLU (rectified linear unit)
y = f(x) = max (0, x), pro x < = 0, y = 0, pro x ≥ 0, y=x

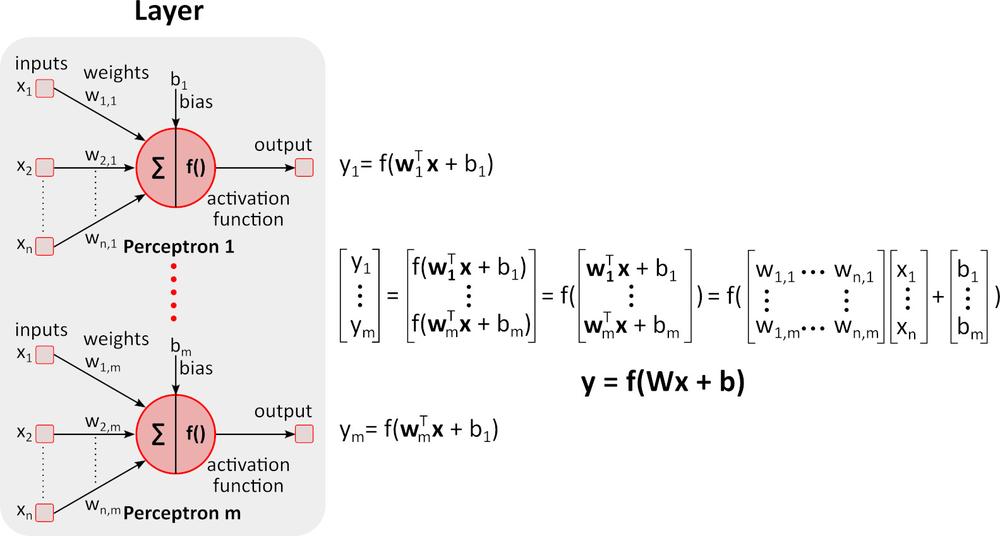
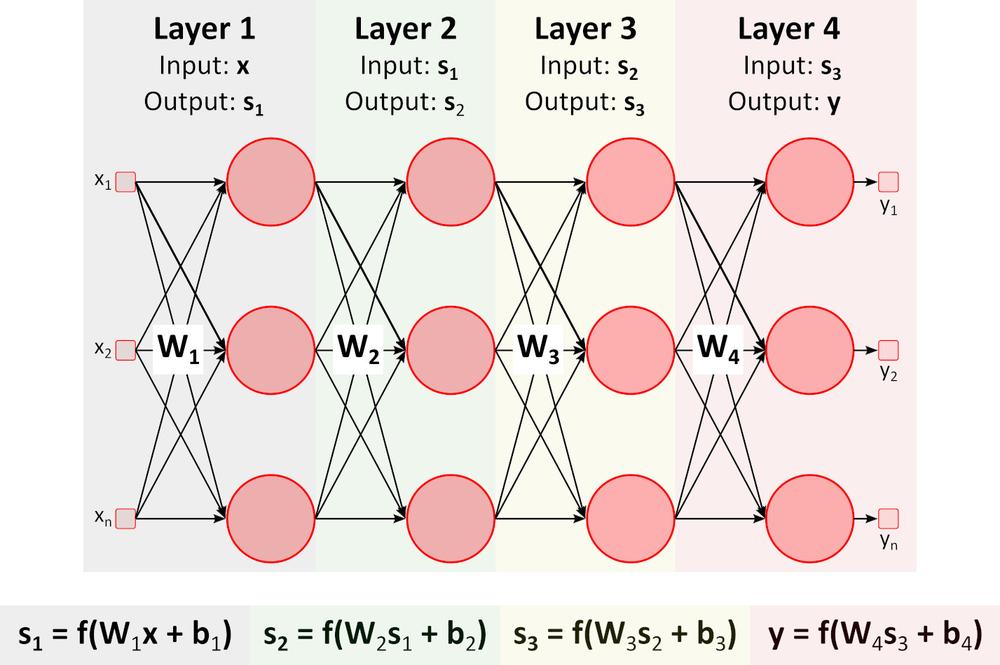
Inference (přechod vpřed)
Obrázek výše zobrazuje hlubokou neuronovou síť (DNN), protože obsahuje více vrstev mezi vstupní a výstupní vrstvou. Všimněte si, že DNN vyžaduje maticové násobení a sčítání. Specializovaný hardware optimalizovaný pro tento úkol, jako například GPU (graphics processing unit) a VPU (vision processing unit) je mnohem rychlejší než univerzální CPU (central processing unit, procesor) a má nižší spotřebu energie.Učení (zpětný přechod)
Řekněme, že chceme DNN naučit rozeznat na fotografii pomeranč, banán, jablko a malinu, tedy třídy objektů.
1. Připravíme velké množství fotografií výše uvedeného ovoce a rozdělíme je na trénovací set a ověřovací set. Trénovací set obsahuje fotografie a správné, požadované výstupy pro tyto fotografie. DNN bude mít 4 výstupy. První výstup poskytuje skóre (pravděpodobnost), že ovoce na obrázku je pomeranč, druhé poskytuje totéž pro banán atd.
2.Nastavíme počáteční hodnoty pro všechny váhy w_i a předpětí b_i. Typicky se používají náhodné hodnoty.
3.Pošleme první obrázek přes DNN. Síť nám poskytne skóre (pravděpodobnost) na každém výstupu. Řekněme, že první obrázek zobrazuje pomeranč. Výstupy z DNN budou y = (pomeranč, banán, jablko, malina) = (0,5 0,1 0,3 0,1). DNN "říká", že na prvním obrázku je pomeranč s pravděpodobností 0,5.
4.Definujeme si ztrátovou (chybovou) funkci, která kvantifikuje shodu mezi předpovídaným skóre a skutečným skóre. Často se používá funkce E = 0.5*sum (e_j)^2, kde e_j = y_j-y_real_j a j je počet fotografií v trénovacím setu. E_1_pomeranč = 0.5*(0.5-1)^2=0.125, E_1_banán =.0.5*(0.1-0)^2 = 0.005 E_1_jablko = 0.5*(0.3-0)^2 = 0.045, E_1_malina = 0.5*(0.1-0)^2 = 0.005 E_1 = (0,125 0,005 0,045 0,005)
5.Pošleme všechny zbývající fotografie z tréninkového setu přes DNN a vypočítáme ztrátovou funkci pro celý set, E (E_pomeranč E_ banán E_jablko E_malina)
6.Abychom modifikovali všechny váhy w_i a předpětí b_i pro následující trénovací přechod (epochu), potřebujeme vědět vliv každého parametru w_i a b_i na ztrátovou funkci pro každou třídu. Pokud zvýšení hodnoty parametru zvýší hodnotu ztrátové funkce, musíme tento parametr snížit a naopak. Jak ale vypočítáme potřebné zvýšení nebo snížení hodnoty parametrů?
Zkusme jednoduchý příklad.
Máme tři body se souřadnicemi (x y): (1 3), (2,5, 2), (3,5 5). Chceme najít takovou přímku y = w.x + b, pro kterou bude ztrátová funkce E = 0.5*sum (e_j)^2, kde e_j = y_j – y_real_j a j=1, 2, 3 minimální. Abychom udělali úkol co nejjednodušší řekněme, že w = 1,2 a potřebujeme najít pouze b. Jako počáteční hodnotu si zvolíme b = 0.
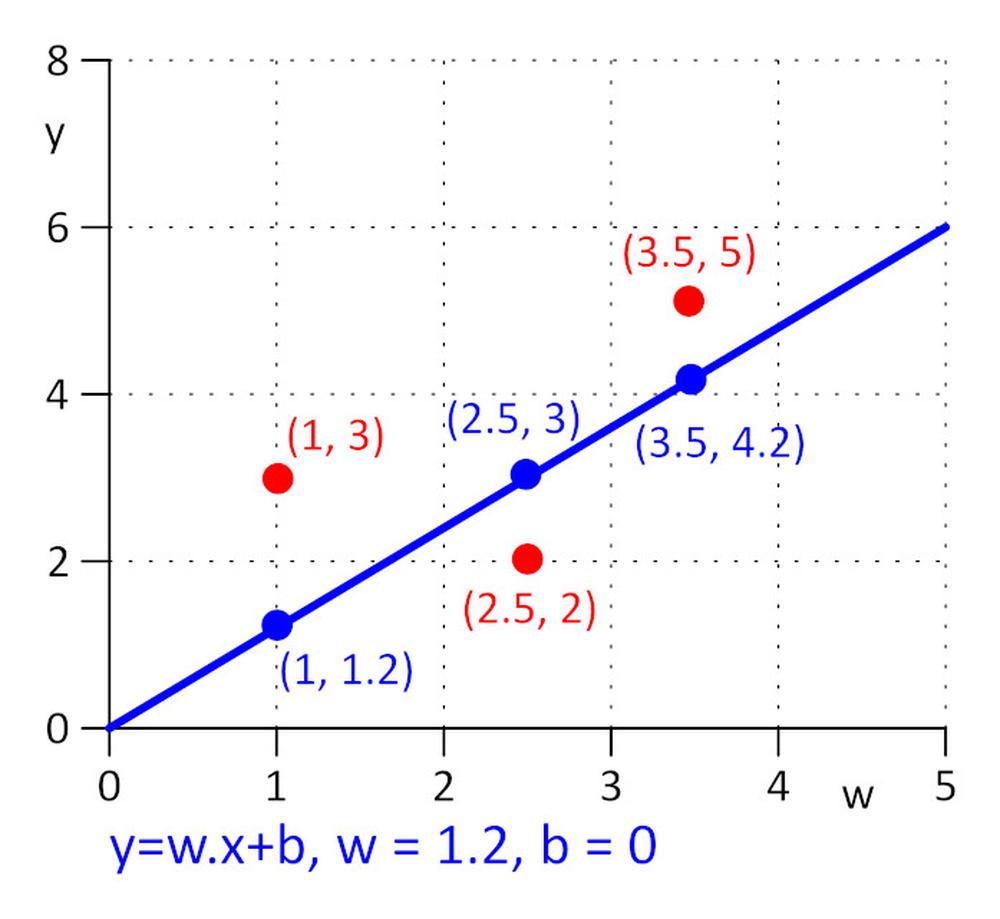
Vypočítejme si ztrátovou funkci E = 0,5*sum ( e_j)^2 = 0,5*(e_1^2 + e_2^2 + e_3^2), e_1=1,2*1 + b -3, e_2 = 1,2*2,5 + b – 2, e_3 = 1,2*3,5 + b – 5.
Ztrátová funkce je jednoduchá, minimum E můžeme najít vyřešením rovnice ∂E/∂b = 0. Jedná se o složenou funkci, pro výpočet ∂E/∂b použijeme pravidlo pro derivování složené funkce.
∂E/∂b=0.5*((∂E/∂e_1)*(∂e_1/∂b) + (∂E/∂e_2)*(∂e_2/∂b) + (∂E/∂e_3)*(∂e_3/∂b)) = 0.5*(2*e_1*1 + 2*e_2*1 + 2*e_3*1) = (1.2*1 + b – 3) + (1.2*2.5 + b – 2) + (1.2*3.5 + b – 5) = 0 => b = 0.53333.
V praxi, kde může počet parametrů w_i a b_i dosáhnout milion a více není praktické řešit rovnice ∂E/∂b_i = 0 a ∂E/∂b_i = 0 přímo, místo toho se používá iterativní algoritmus.
Začněme s b = 0. Následující hodnota bude b_1 = b_0 – η*∂E/∂b, kde η je rychlost učení (hyper-parameter) a -η*∂E/∂b je velikost kroku. Učení zastavíme, pokud velikost kroku dosáhla definovaný práh, v praxi 0,001 nebo méně. Pro η = 0,3, b_1 = 0,48, b_2 = 0,528, b_3 = 0,5328, b_4 = 0,53328 a b_5 = 0,5533328. Po pěti iteracích klesla velikost kroku na 4,8e-5 a tady učení zastavíme. Hodnota b získaná tímto algoritmem je prakticky stejná jako hodnota získaná vyřešením rovnice ∂E/∂b=0.
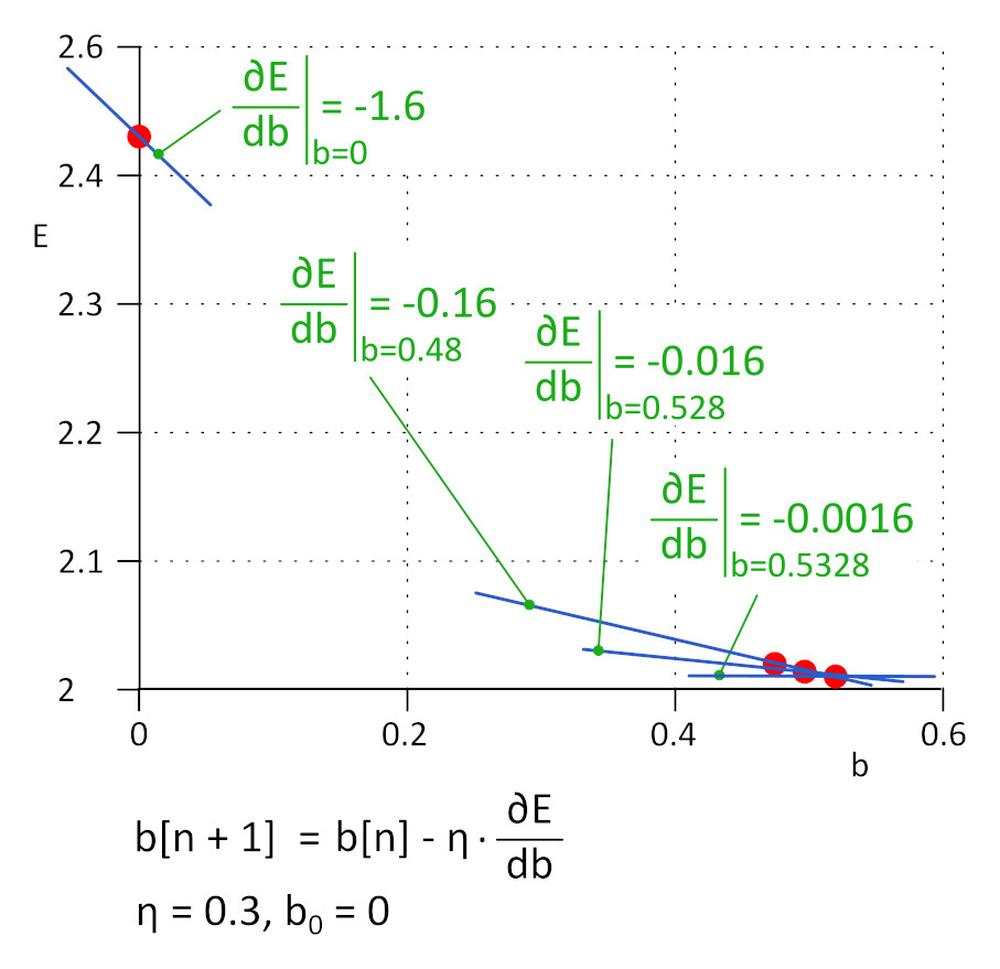
Tato metoda se nazývá metoda klesajícího gradientu.
Rychlost učení je důležitý hyper-parametr. Pokud je příliš malá, pro nalezení minima ztrátové funkce je potřebných mnoho kroků, pokud je příliš velká, algoritmus může selhat. V praxi se používají vylepšené varianty algoritmu jako například Adam.
7. Opakujeme kroky 5 a 6, dokud hodnota ztrátové funkce neklesne na požadovanou hodnotu.
8.Pošleme přes DNN ověřovací set a vyhodnotíme přesnost.
V současnosti je učení DNN vysoce experimentální proces. Je známo mnoho architektur DNN, každá z nich je vhodná pro specifický rozsah úkolů. Každá DNN architektura má svůj vlastní set hyper-parametrů, které ovlivňují její chování. Vyzbrojte se trpělivostí a výsledek se dostaví..
Více informací o produktech AAEON vám rádi poskytneme na adrese aaeon@soselectronic.cz
Líbí se Vám naše články? Nezmeškejte už ani jeden z nich! Nemusíte se o nic starat, my zajistíme doručení až k Vám.