Prečo teraz?

Pri súčasnom stave technológie dokážeme natrénovať hlbokú neurónovú sieť (DNN) pre špecifické úlohy ako je detekcia a rozpoznávanie objektov a ľudskej tváre, rozpoznávanie reči, preklad jazyka, hry (šach, go atď.), autonómne riadenie vozidla, sledovanie stavu senzorov a rozhodovanie o prediktívnej údržbe strojov, vyhodnocovanie röntgenových snímok v zdravotníctve atď. Pre takéto špecializované úlohy môže DNN dosiahnuť alebo dokonca prevýšiť ľudské schopnosti.
Prečo používať umelú inteligenciu na okraji siete
Napríklad, moderná budova obsahuje množstvo snímačov, vzduchotechnických zariadení, výťahov, bezpečnostných kamier atď. Z dôvodov bezpečnosti, latencie alebo robustnosti je vhodnejšie, aby úlohy umelej inteligencie bežali lokálne, na okraji lokálnej siete, a posielať do cloudu iba anonymizované údaje, ktoré sú potrebné na prijímanie globálnych rozhodnutí.
Hardvér na okraji siete
Pre nasadenie DNN na okraji siete potrebujeme zariadenie s dostatočným výpočtovým výkonom a súčasne s nízkou spotrebou energie. Súčasný stav technológie ponúka kombináciu CPU s nízkym príkonom a VPU akcelerátorom (x86 CPU SBC+ Intel Myriad X VPU) alebo CPU + GPU (ARM CPU + Nvidia GPU)
Najjednoduchším spôsobom ako začať s DNN je použiť UP Squared AI Vision X Developer Kit verziu B. Kit je založený na procesore UP Square SBC s procesorom Intel Atom®X7-E3950, 8GB RAM, 64GB eMMC, Myriad X MA2485 VPU a USB kameru s rozlíšením 1920 x 1080 a manuálnym zaostrovaním. Na kite je predinštalovaná distribúcia Ubuntu 16.04 (kernel 4.15) a OpenVINO toolkit 2018 R5.
Toolkit obsahuje prekompilované demo aplikácie v zložke /home/upsquared/build/intel64/Release a pretrénované modely v zložke /opt/intel/computer_vision_sdk/deployment_tools/intel_models. Ak chcete zobraziť pomôcky pre akúkoľvek demo aplikáciu, spustite ju v termináli s voľbou –h. Pred spustením aplikácie je potrebné inicializovať prostredie OpenVINO príkazom source /opt/intel/computer_vision_sdk/bin/setupvars.sh.
Okrem UP Squared AI Vision X Developer Kitu AAEON ponúka:
1.Moduly založené na Myriad X MA2485 VPU: AI Core X (mPCIe full-size, 1x Myriad X), AI Core XM 2280 (M.2 2280 B+M key, 2x Myriad X), AI Core XP4/ XP8 (PCIE [x4] karta, 4 alebo 8x Myriad X).
2.Sériu BOXER-8000 založenú na module Nvidia Jetson TX2.
3.BOXER-8320AI s procesorom Core i3-6100U alebo Celeron 3955U a dvoma AI Core X modulmi.
4.Sériu Boxer-6841M s matičnou doskou pre procesory Intel Core-I alebo Xeon 6-tej / 7-mej generácie pre päticu LGA1151 a 1x PCIe [x16] alebo 2x PCIe [x8] sloty pre GPU s max. príkonom 250W.
Hardvér pre učenie
Pre trénovanie DNN potrebujeme vysoký výpočtový výkon. Napríklad na súťaži ImageNet v roku 2012 víťazný tím použil konvolučnú neurónovú sieť AlexNet. Pre učenie bolo potrebných 1.4 ExaFLOP = 1,4e6 TFLOP operácií. Učenie zabralo 5 až 6 dní na dvoch Nvidia GTX580 GPU, kde každá mala výpočtový výkon 1,5 TFLOPS.Nasledujúca tabuľka sumarizuje teoretický špičkový výkon hardvéru.
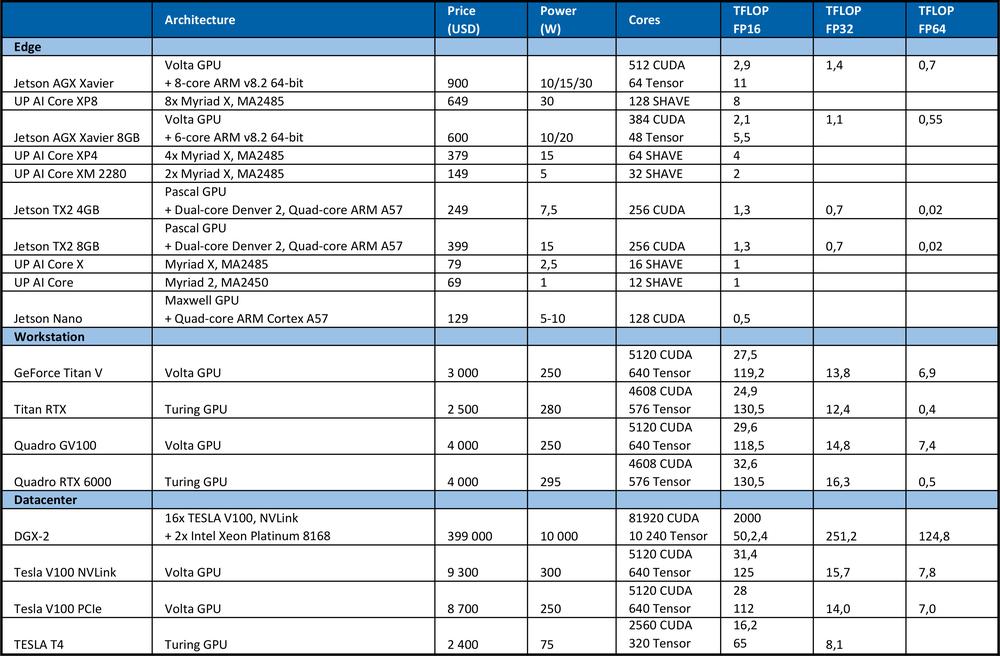
Pre porovnanie, špičkový procesor Intel Xeon Platinum 8180
●má 28 jadier s dvomi AVX-512 & FMA jednotkami na jadro
●AVX-512 turbo frekvenciu 2,3GHz, ak sú aktívne všetky jadrá
●stojí 10 000 USD.
Ponúka teoretický špičkový výkon: počet jadier * frekvencia v GHz * AVX-512 DP FLOPS/Hz * počet AVX-512 jednotiek * 2 = 2060.8 GFLOPS v dvojnásobnej presnosti (DP) → 4,1216 TFLOPS v jednoduchej presnosti (32-bit).
Ako môžete vidieť z tabuľky vyššie, GPU poskytuje oveľa viac výkonu pre učenie neurónových sietí. Je potrebné poznamenať, že počet operácií za sekundu nie je jediným parametrom, ktorý vplýva na rýchlosť učenia. Faktory ako veľkosť RAM, rýchlosť prenosu dát medzi CPU a RAM, GPU a GPU RAM a medzi jednotlivými GPU tiež ovplyvňuje rýchlosť učenia.
Softvér

OpenVINO
OpenVINO (open visual inference and neural network) je bezplatný softvér, ktorý umožňuje rýchle nasadenie aplikácií a riešení, ktoré napodobňujú ľudské videnie.
OpenVINO toolkit:
●Používa CNN (convolution neural network)
●Dokáže rozdeliť výpočty medzi Intel CPU, integrovanú GPU, Intel FPGA, Intel Movidius Neural Compute Stick a akcelerátory s Intel Movidius Myriad VPUs
●Poskytuje optimalizované rozhranie pre OpenCV, OpenCL a OpenVX
●Podporuje Caffe, TensorFlow, MXNet, ONNX, Kaldi frameworky
TensorFlow
TensorFlow je open source knižnica pre numerické výpočty a strojové učenie. Poskytuje pohodlné front-end API pre vytváranie aplikácií v programovacom jazyku Python, samotná aplikácia vygenerovaná knižnicou TensorFlow je ale prekonvertovaná do optimalizovaného kódu v C++, ktorá po skompilovaní môže bežať na rôznych platformách ako sú CPU, GPU, lokálny počítač, klastri v cloude, embedded zariadeniach na okraji siete a podobne.
Ostatný užitočný softvér:
Jupyter Lab / Notebook
https://jupyter.org/index.html
https://github.com/jupyter/jupyter/wiki/Jupyter-kernels
https://jupyterlab.readthedocs.io/en/stable
Keras
Pandas
MatplotLib
Numpy
Ako to funguje?
Zjednodušený model neurónu
Zjednodušený model neurónu – perceptron bol po prvý krát popísaný Warrenom McCullochom a Walterom Pittsom a platí stále za referenčnú normu v oblasti neurónových sietí.
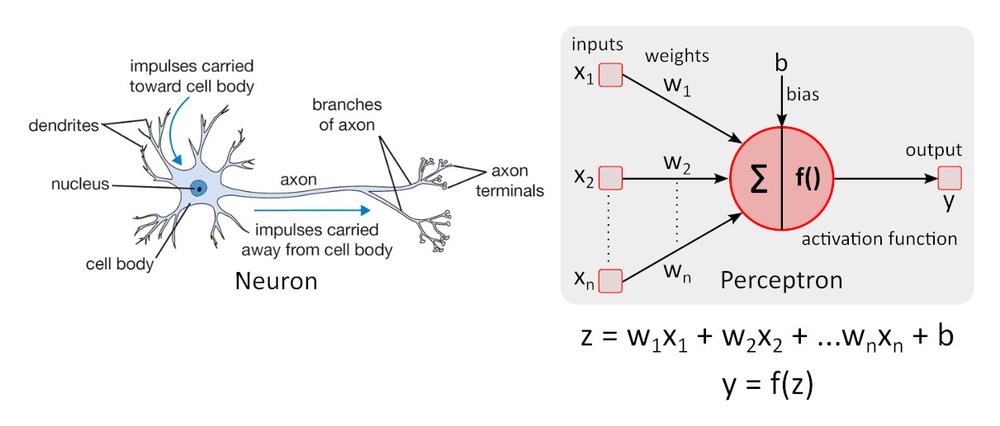
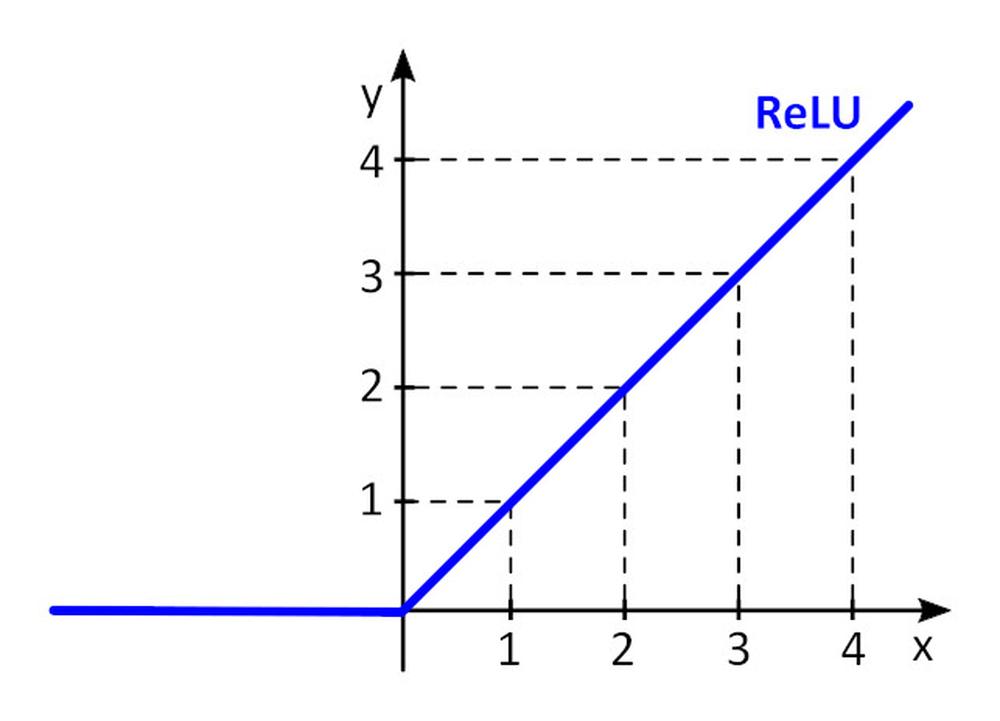
Aktivačná funkcia f () pridáva do perceptronu nelinearitu. Bez nelineárnej aktivačnej funkcie v neurónovej sieti (NN) zloženej z perceptronov, bez ohľadu na to, koľko vrstiev by mala, správala by sa ako jednovrstvový perceptron, pretože sčítanie týchto vrstiev by nám poskytlo len ďalšiu lineárnu funkciu. Najčastejšie používanou aktivačnou funkciou je ReLU (rectified linear unit)
y = f(x) = max (0, x), pre x < = 0, y = 0, pre x ≥ 0, y=x

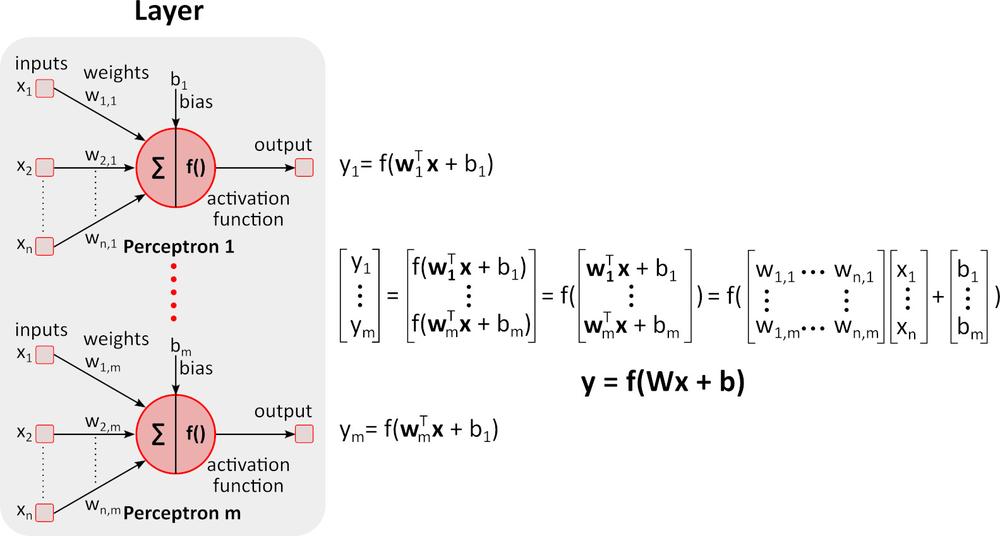
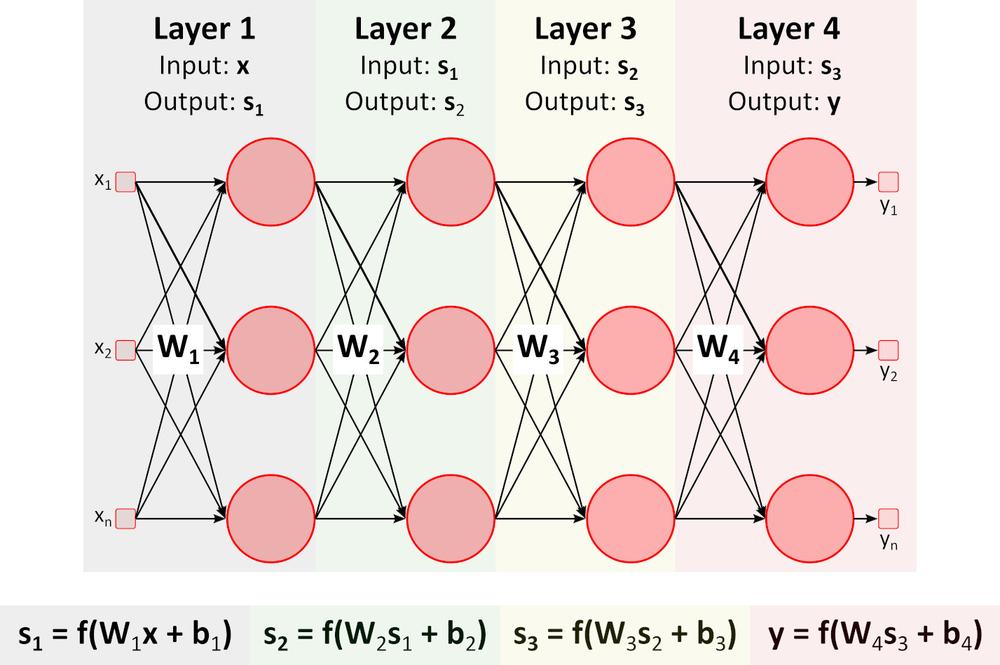
Inferencia (Prechod vpred)
Obrázok vyššie zobrazuje hlbokú neurónovú sieť (DNN), pretože obsahuje viac vrstiev medzi vstupnou a výstupnou vrstvou. Všimnite si že, DNN vyžaduje maticové násobenia a sčítanie. Špecializovaný hardvér optimalizovaný pre túto úlohu, ako napríklad GPU (graphics processing unit) a VPU (vision processing unit), je oveľa rýchlejší ako univerzálna CPU (central processing unit, procesor) a má nižšiu spotrebu energie.Učenie (Spätný prechod)
Povedzme, že chceme DNN naučiť na fotografii rozoznať pomaranč, banán, jablko a malinu, teda triedy objektov.
1. Pripravíme veľké množstvo fotografií horeuvedeného ovocia a rozdelíme ich na trénovací set a overovací set. Trénovací set obsahuje fotografie a správne, požadované výstupy pre tieto fotografie. DNN bude mať 4 výstupy. Prvý výstup poskytuje skóre (pravdepodobnosť), že ovocie na obrázku je pomaranč, druhé poskytuje to isté pre banán atď.
2.Nastavíme počiatočné hodnoty pre všetky váhy w_i a predpätia b_i. Typicky sa používajú náhodné hodnoty.
3.Pošleme prvý obrázok cez DNN. Sieť nám poskytne skóre (pravdepodobnosť) na každom výstupe. Povedzme, že prvý obrázok zobrazuje pomaranč. Výstupy z DNN budú y = (pomaranč, banán, jablko, malina) = (0,5 0,1 0,3 0,1). DNN “hovorí”, že na prvom obrázku je pomaranč s pravdepodobnosťou 0,5.
4.Definujeme si stratovú (chybovú) funkciu, ktorá kvantifikuje zhodu medzi predpovedaným skóre a skutočným skóre. Často sa používa funkcia E = 0.5*sum (e_j)^2, kde e_j = y_j-y_real_j a j je počet fotografií v trénovacom sete. E_1_pomaranč = 0.5*(0.5-1)^2=0.125, E_1_banán =.0.5*(0.1-0)^2 = 0.005 E_1_jablko = 0.5*(0.3-0)^2 = 0.045, E_1_malina = 0.5*(0.1-0)^2 = 0.005 E_1 = (0,125 0,005 0,045 0,005)
5.Pošleme všetky zostávajúce fotografie z trénovacieho setu cez DNN a vypočítame stratovú funkciu pre celý set, E (E_pomaranč E_ banán E_jablko E_malina)
6.Aby sme modifikovali všetky váhy w_i a predpätia b_i pre nasledujúci trénovací prechod (epochu) potrebujeme vedieť vplyv každého parametra w_i a b_i na stratovú funkciu pre každú triedu. Ak zvýšenie hodnoty parametra zvýši hodnotu stratovej funkcie, musíme tento parameter znížiť a naopak. Ako ale vypočítame potrebné zvýšenie alebo zníženie hodnoty parametrov?
Skúsme jednoduchý príklad.
Máme tri body so súradnicami (x y): (1 3), (2,5, 2), (3,5 5). Chceme nájsť takú priamku y = w.x + b, pre ktorú bude stratová funkcia E = 0.5*sum (e_j)^2, kde e_j = y_j – y_real_j a j=1, 2, 3 minimálna. Aby sme urobili úlohu čo najjednoduchšou povedzme, že w = 1,2 a potrebujeme nájsť iba b. Ako počiatočnú hodnotu si zvolíme b = 0.
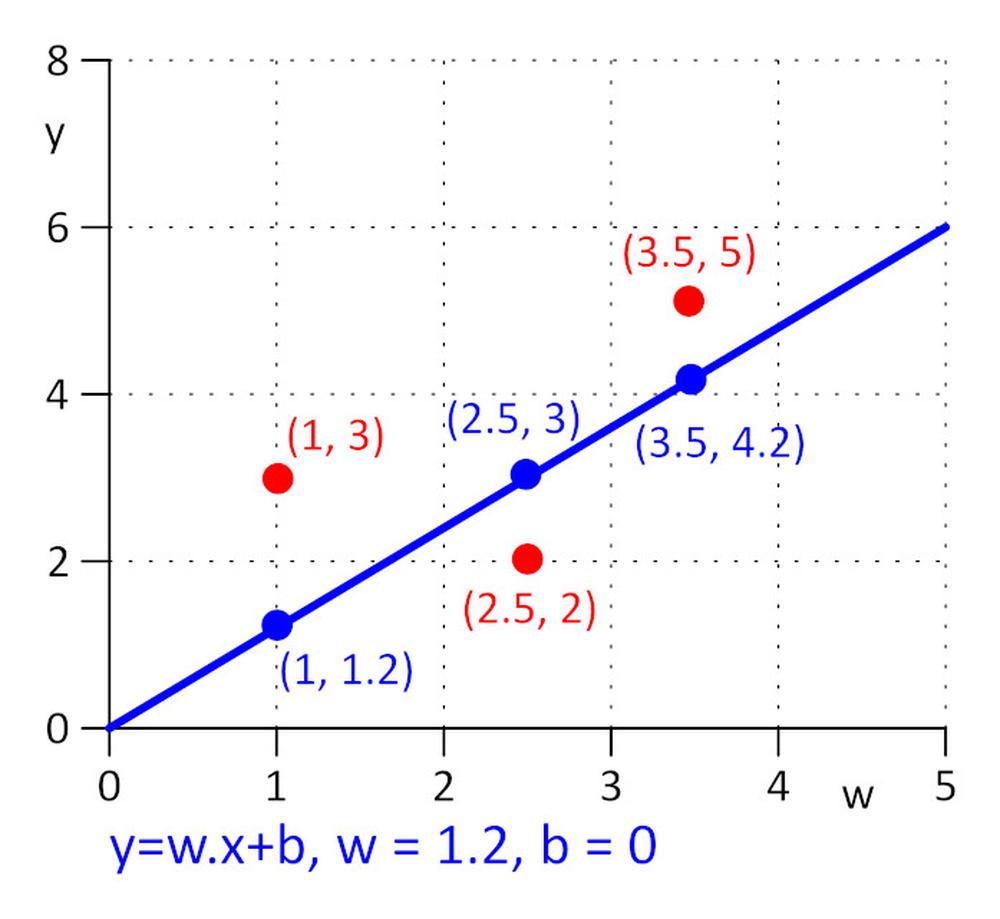
Vypočítajme si stratovú funkciu E = 0,5*sum ( e_j)^2 = 0,5*(e_1^2 + e_2^2 + e_3^2), e_1=1,2*1 + b -3, e_2 = 1,2*2,5 + b – 2, e_3 = 1,2*3,5 + b – 5.
Stratová funkcia je jednoduchá, minimum E môžeme nájsť vyriešením rovnice ∂E/∂b = 0. Jedná sa o zloženú funkciu, pre výpočet ∂E/∂b použijeme pravidlo pre derivovanie zloženej funkcie.
∂E/∂b=0.5*((∂E/∂e_1)*(∂e_1/∂b) + (∂E/∂e_2)*(∂e_2/∂b) + (∂E/∂e_3)*(∂e_3/∂b)) = 0.5*(2*e_1*1 + 2*e_2*1 + 2*e_3*1) = (1.2*1 + b – 3) + (1.2*2.5 + b – 2) + (1.2*3.5 + b – 5) = 0 => b = 0.53333.
V praxi, kde počet parametrov w_i a b_i môže dosiahnuť milión a viac nie je praktické riešiť rovnice ∂E/∂b_i = 0 a ∂E/∂b_i = 0 priamo, namiesto toho sa používa iteračný algoritmus.
Začneme s b = 0. Nasledujúca hodnota bude b_1 = b_0 – η*∂E/∂b, kde η je rýchlosť učenia (hyper-parameter) a -η*∂E/∂b je veľkosť kroku. Učenie zastavíme, ak veľkosť kroku dosiahla definovaný prah, v praxi 0,001 alebo menej. Pre η = 0,3, b_1 = 0,48, b_2 = 0,528, b_3 = 0,5328 and b_4 = 0,53328 a b_5 = 0,5533328. Po piatich iteráciách veľkosť kroku klesla na 4,8e-5 a tu učenie zastavíme. Hodnota b získaná týmto algoritmom je prakticky rovnaká ako hodnota získaná vyriešením rovnice ∂E/∂b=0.
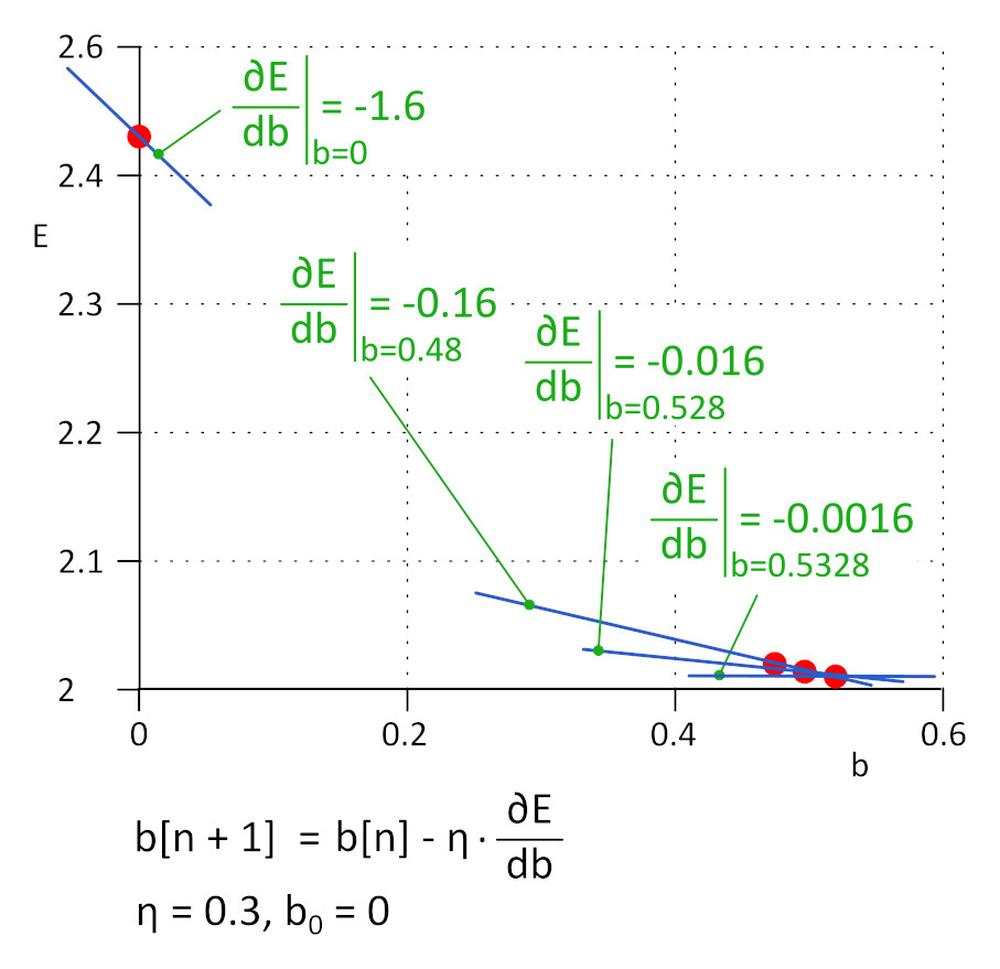
Táto metóda sa nazýva metóda klesajúceho gradientu.
Rýchlosť učenia je dôležitý hyper-parameter. Ak je príliš malá, na nájdenie minima stratovej funkcie je potrebných veľa krokov, ak je príliš veľká, algoritmus môže zlyhať. V praxi sa používajú vylepšené varianty algoritmu ako napríklad Adam.
7.Opakujeme kroky 5 a 6 dovtedy, kým hodnota stratovej funkcie klesne na požadovanú hodnotu.
8.Pošleme cez DNN overovací set a vyhodnotíme presnosť.
V súčasnosti je učenie DNN vysoko experimentálny proces. Je známych mnoho architektúr DNN, každá z nich je vhodná pre špecifický rozsah úloh. Každá DNN architektúra má svoj vlastný set hyper-parametrov, ktoré ovplyvňujú jej správanie. Vyzbrojte sa trpezlivosťou a výsledok sa dostaví.
Viac informácií o produktoch AAEON, vám radi poskytneme na adrese aaeon@soselectronic.com
Páčia sa Vám naše články? Nezmeškajte už ani jeden z nich!
Nemusíte sa o nič starať, my zabezpečíme doručenie až k Vám.




