De ce acum?

În starea curentă a tehnologiei putem instrui rețele neuronale profunde (DNN) pentru anumite sarcini, cum ar fi detectarea și recunoașterea obiectelor și a chipurilor omenești, recunoașterea vocii, traducere, jocuri (șah, go etc.), conducerea autonomă a vehiculelor, monitorizarea statutului unui senzor și deciziile de întreținere predictivă a mașinii, evaluarea imaginilor X în sănătate etc. Pentru astfel de sarcini specializate, un DNN poate atinge sau chiar depăși capacitățile umane.
De ce să folosim inteligența artificială la margine
De exemplu, clădirile moderne conțin mulți senzori, dispozitive HVAC, lifturi, camere de securitate, etc. conectate la o rețea internă. Din motive de securitate, latență sau robustețe, este mai adecvată rularea sarcinilor de inteligență artificială local, la marginea unei rețele locale, trimițând doar datele anonime care sunt necesare pentru a duce o decizie globală în cloud.
Hardware pe margine
Pentru a implementa DNN pe margine avem nevoie de un dispozitiv cu suficientă putere de calcul, dar în același timp și cu un consum suficient de mic. Starea actuală a tehnologiei oferă o combinație între CPU de mică putere și accelerator VPU (x86 CPU SBC+ Intel Myriad X VPU) sau CPU + accelerator GPU (ARM CPU + Nvidia GPU).
Cea mai simplă metodă de a porni DNN este folosind UP Squared AI Vision X Developer Kit versiunea B. Se bazează pe UP Square SBC cu procesor Intel Atom®X7-E3950 cu 8GB RAM, 64 GB eMMC, modul AI Core X cu Myriad X MA2485 VPU și cameră USB cu rezoluție 1920 x 1080 și focus manual. Kitul are preinstalat Ubuntu 16.04 (kernel 4.15) și OpenVINO toolkit 2018 R5.
Toolkitul conține aplicații demo precompilate în /home/upsquared/build/intel64/Release și modele pre-antrenate în /opt/intel/computer_vision_sdk/deployment_tools/intel_models. Pentru a vedea modulul ajutor în orice aplicație demo, rulați-o în terminal cu opțiunea –h. Se recomandă inițializarea mediului OpenVINO înainte de a rula aplicația demo prin comanda source /opt/intel/computer_vision_sdk/bin/setupvars.sh.
Pe lângă kit-ul UP Squared AI Vision X Developer, AAEON mai oferă și:
1. Module Myriad X MA2485 pe bază de VPU: AI Core X (mPCIe full-size, 1x Myriad X), AI Core XM 2280 (M.2 2280 B+M key, 2x Myriad X), AI Core XP4/ XP8 (PCIE [x4] card, 4 sau 8x Myriad X).
2.Seria BOXER-8000 pe bază de modul Nvidia Jetson TX2.
3.BOXER-8320AI cu procesor Core i3-6100U sau Celeron 3955U și 2 module AI Core X.
4.Seria Boxer-6841M cu placă de bază pentru Intel generația 6th / 7th de Core-I sau procesor Xeon pentru socket LGA1151 și 1x PCIe [x16] sau 2x PCIe [x8] sloturi pentru GPU cu consum maxim de putere de 250W.
Hardware pentru învățare
Pentru a instrui DNN avem nevoie de o mare putere de calcul. De exemplu, la competiția ImageNet din 2012, echipa câștigătoare a folosit rețeaua neuronală convoluțională AlexNet. Au fost necesare operațiuni 1.4ExaFLOP=1,4e6 TFLOP pentru învățare. Au fost necesare între 5 și 6 zile pe două GPU-uri Nvidia GTX 580, fiecare având performanță de calcul de 1.5 TFLOP.Tabelul de mai jos rezumă performanța maximă teoretică a hardware-ului.
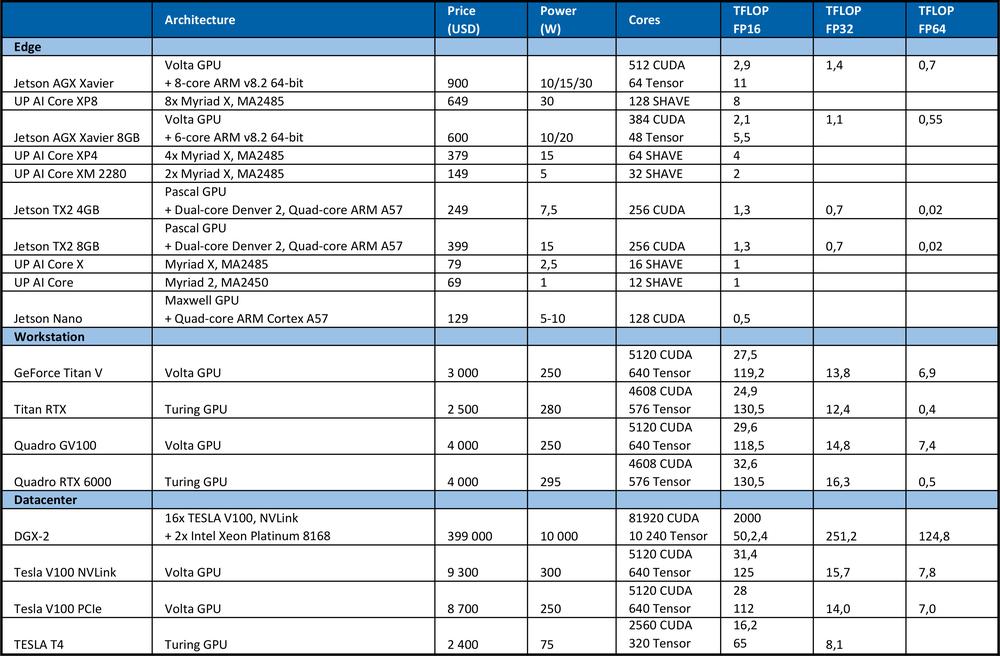
Pentru comparație, procesorul de foarte bună calitate Intel Xeon Platinum 8180
● Are 28 de nuclee cu 2 unități AVX-512 & FMA per nucleu
●AVX-512 frecvență turbo 2.3GHz dacă toate nucleele sunt active
●Costă USD 10 000
Oferă o performanță maximă teoretică: # de nuclee * frecvență în GHz * AVX-512 DP FLOPS/Hz * # de AVX-512 unități * 2 = 2060.8 GFLOPS în precizie dublă (DP) → 4.1216 TFLOPS unic (32-bit).
După cum puteți vedea din tabelul de mai sus, GPU oferă o mult mai bună performanță pentru învățarea rețelelor neuronale. Este necesar să notăm faptul că numărul de operațiuni pe secundă nu este singurul parametru care afectează performanța de învățare. Factorii precum dimensiunea RAM-ului, rata de transfer a datelor dintre CPU și RAM, GPU și GPU RAM sau între GPU influențează, de asemenea, viteza de învățare.
Software

OpenVINO
Toolkit-ul OpenVINO (interfață vizuală deschisă și rețea neuronală) este un software gratuit care permite implementarea rapidă a aplicațiilor și a soluțiilor care emulează viziunea umană.
Toolkit-ul OpenVINO toolkit:
●Folosește CNN (rețeaua neuronală convoluțională)
●Poate împărți volumul de calcul între Intel CPU, GPU-ul integrat, Intel FPGA, Intel Movidius Neural Compute Stick și acceleratoarele de vedere cu Intel Movidius Myriad VPUs
●Oferă o interfață optimizată pentru OpenCV, OpenCL și OpenVX
●Suportă framework-urile Caffe, TensorFlow, MXNet, ONNX, Kaldi
TensorFlow
TensorFlow este o librărie open source pentru calcul numeric și învățare artificială. Oferă un front-end API convenabil pentru construirea aplicațiilor în limba de programare Python. Cu toate acestea, aplicația generată de TensorFlow în sine este convertită într-un cod C ++ optimizat care poate rula pe o varietate de platforme, cum ar fi CPU-uri, GPU-uri, mașini locale, cluster în cloud, dispozitive integrate la margine și altele similare.
Alte Software-uri utile
Jupyter Lab / Notebook
https://jupyter.org/index.html
https://github.com/jupyter/jupyter/wiki/Jupyter-kernels
https://jupyterlab.readthedocs.io/en/stable
Keras
Pandas
MatplotLib
Numpy
Cum funcționează
Model neuronal simplificat
Modelul neuronal simplu – perceptronul a fost pentru prima dată descris de către Warren McCulloch și Walter Pitts în 1943 și reprezintă în continuare standardul de referință în domeniul rețelelor neuronale.
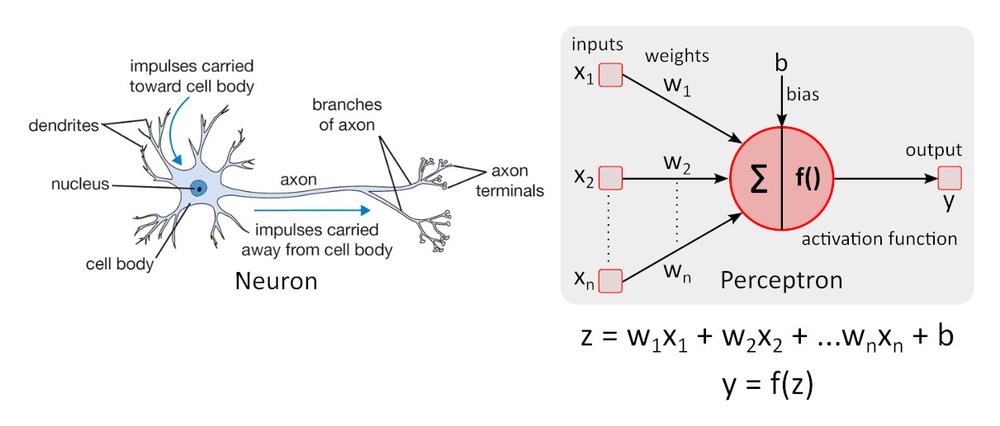
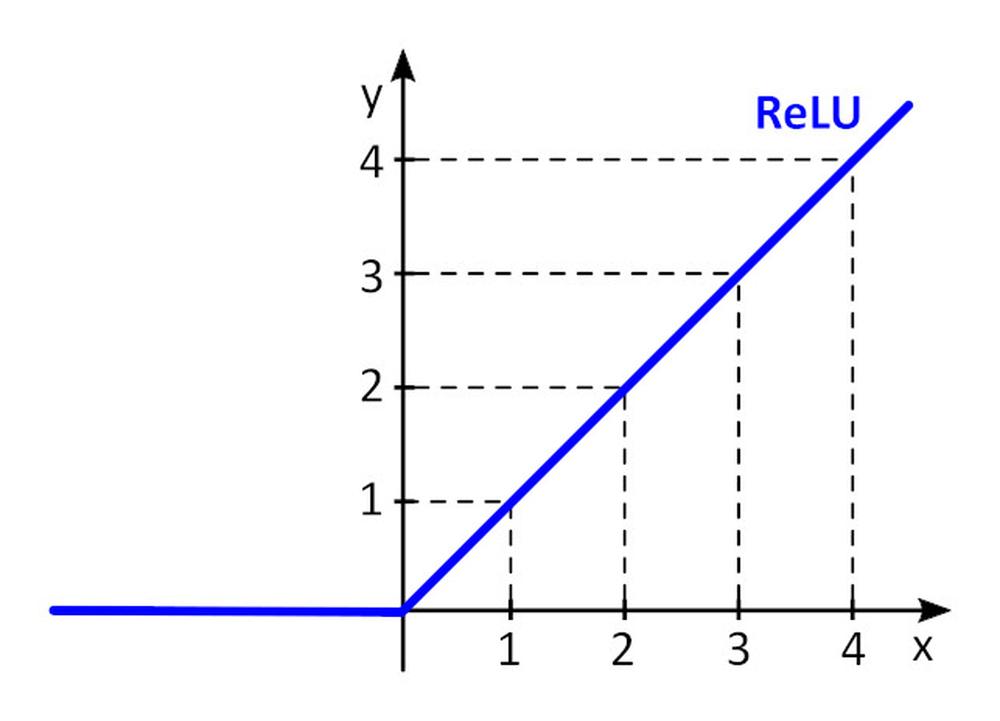
Funcția de activare f () oferă neliniaritatea perceptronului. Fără funcția de activare non-liniară din rețeaua neuronală (NN) a perceptronilor, indiferent câte straturi ar avea, s-ar comporta exact ca un perceptron cu strat unic, deoarece adunarea acestor straturi v-ar da doar o altă funcție liniară. Cea mai des folosită funcție de activare este unitatea liniară rectificată– ReLU.
y = f(x) = max (0, x), unde x < = 0, y = 0, unde x ≥ 0, y=x

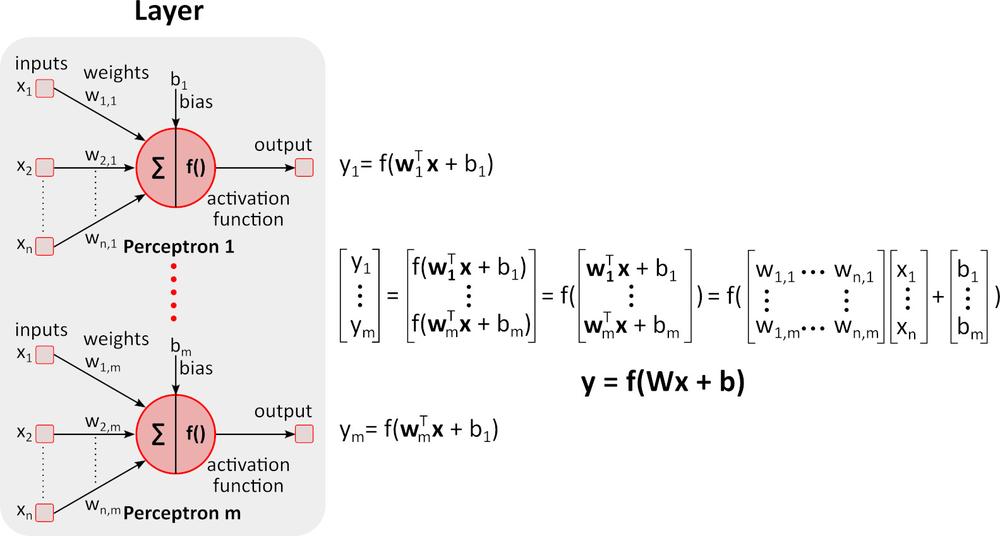
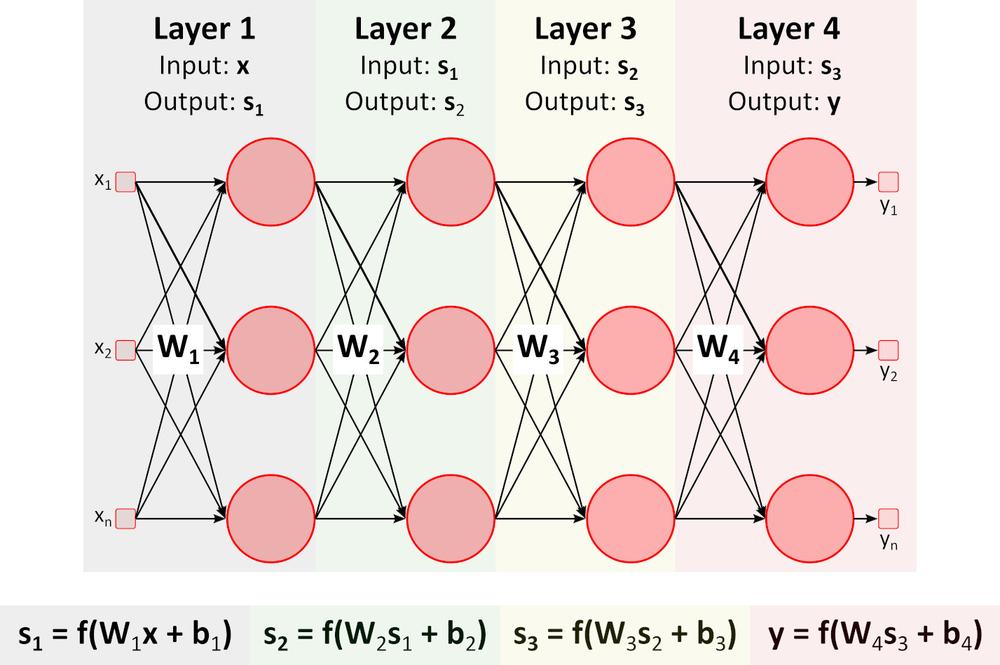
Învățare (Backward pass)
Figura de mai sus prezintă o rețea neuronală profundă (DNN) deoarece conține multiple staturi între straturile de intrare și straturile de ieșire. După cum puteți observa, DNN necesită multiplicări și adunări matriceale. Hardware-ul special optimizat pentru această sarcină, cum ar fi GPU (unitatea de procesare grafică) VPU (unitatea de procesare vizuală), este mult mai rapid decât CPU-ul (unitate centrală de procesare, procesor) de uz general, având, de asemenea, și un consum mai mic de putere.Învățare (Backward pass)
Să spunem că dorim să învățăm DNN cum să recunoască portocala, banana, mărul și zmeura (clase de obiecte) din imagine.
1. Am pregătit un lot de imagini cu fucte mai sus și l-am împărțit în set de instruire și set de validare. Setul de instruire conține imagini și rezultatele corecte, necesare, pentru aceste imagini. DNN va avea 4 ieșiri. Prima ieșire oferă scorul (probabilitatea) ca fructul din imagine să fie portocală, cea de a doua oferă același lucru în cazul bananei etc.
2.Am stabilit valori inițiale pentru toate ponderile w_i și bias-urile b_i. De obicei se folosesc valori aleatoare.
3.Am trecut prima imagine prin DNN. Rețeaua oferă scoruri (probabilități) pentru fiecare ieșire. Să spunem că prima imagine prezintă o portocală. Ieșirile rețelei pot fi y= (portocală, banană, măr, zmeură) = (0.5, 0.1, 0.3, 0.1). Rețeaua “spune” că intrarea este portocală, cu o probabilitate de 0.5.
4.Definim o funcție de pierdere (eroare) care cuantifică acordul dintre scorurile prezise și scorurile corecte pentru fiecare clasă. Funcția E = 0.5*sum (e_j) ^2, unde e_j = y_j - y_real_j și j este numărul de imagini din setul de instruire este deseori folosită. E_1_orange = 0.5*(0.5-1)^2=0.125, E_1_banana =.0.5*(0.1-0)^2 = 0.005 E_1_apple = 0.5*(0.3-0)^2 = 0.045, E_1_raspberry = 0.5*(0.1-0)^2 = 0.005 E_1 = (0.125, 0.005, 0.045, 0.005)
5.Trecem toate celelalte imagini din setul de instruire prin DNN și calculăm E (E_orange, E_banana, E_apple, E_raspberry) valoarea funcției de pierdere pentru întregul set de instruire.
6.Pentru a modifica toate ponderile w_i și bias-urile b_i pentru următoarea sesiune de training (epocă), trebuie să cunoaștem influența fiecărui parametru w_i și b_i față de funcția de pierdere pentru fiecare clasă. În cazul în care creșterea valorii parametru cauzează creșterea valorii funcției de pierdere, avem nevoie să descreștem acest parametru și vice versa. Însă cum calculăm necesarul de creștere și descreștere al parametrilor?
Să încercăm un exemplu simplu.
Avem trei puncte cu coordonate (x, y): (1, 3), (2.5, 2), (3.5, 5). Dorim să găsim o linie y = w.x + b pentru care funcția de pierdere E = 0.5*sum (e_j) ^2 , unde e_j = y_j – y_real_j, j=1, 2, 3 este minim. Pentru a face sarcina cât mai simplă posibil, să spunem că w=1.2 și avem nevoie să găsim valoarea optimă doar pentru b. Alegem valoarea inițială pentru b=0.
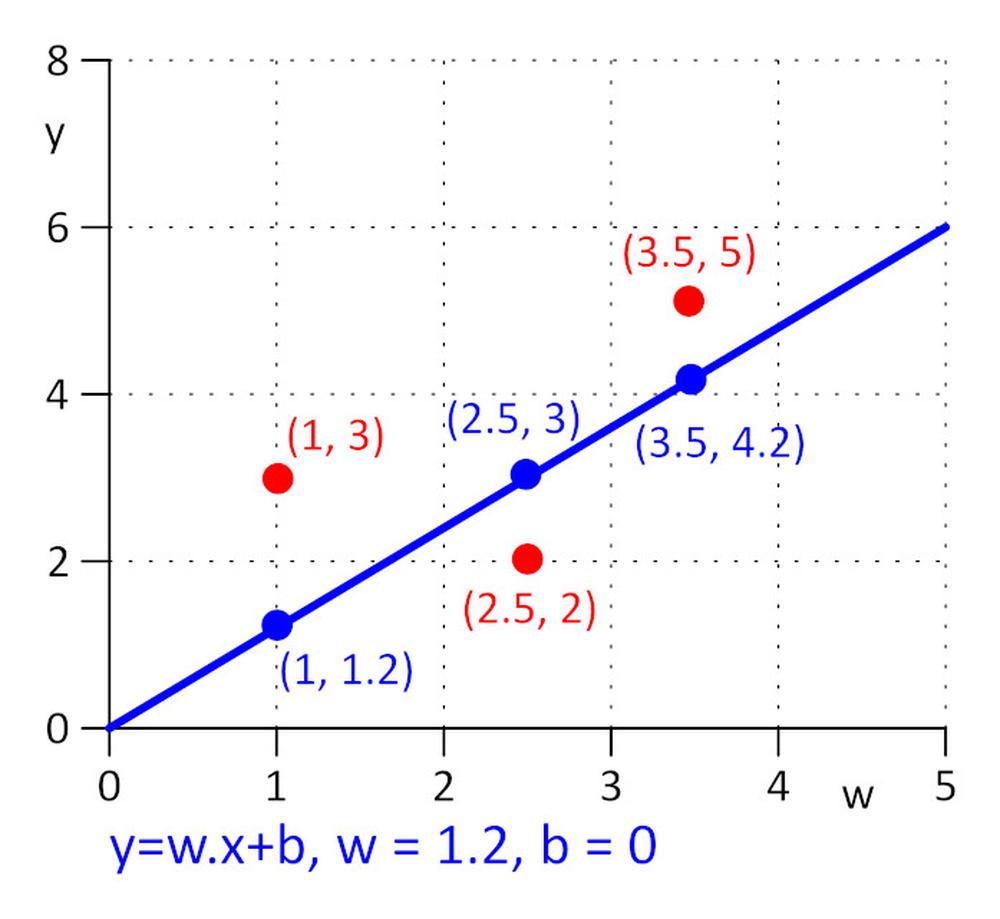
Să calculăm funcția de pierdere: E = 0.5*sum (e_j) ^2 = 0.5*(e_1^2 + e_2^2 + e_3^2), e_1=1.2*1 + b -3, e_2 = 1.2*2.5 + b – 2, e_3 = 1.2*3.5 + b – 5.
Funcția de pierdere E este simplă, putem găsi un E minim rezolvând ecuația: ∂E/∂b = 0. Este o funcție compusă, pentru a calcula ∂E/∂b aplicăm regula lanțului.
∂E/∂b=0.5*((∂E/∂e_1)*(∂e_1/∂b) + (∂E/∂e_2)*(∂e_2/∂b) + (∂E/∂e_3)*(∂e_3/∂b)) = 0.5*(2*e_1*1 + 2*e_2*1 + 2*e_3*1) = (1.2*1 + b – 3) + (1.2*2.5 + b – 2) + (1.2*3.5 + b – 5) = 0 => b = 0.53333
În practică, acolo unde numărul de parametri w_i și b_i poate ajunge la un milion sau peste, rezolvarea directă a ecuațiilor ∂E/∂b_i = 0 și ∂E/∂b_i = 0 nu este practică, iar în loc se folosește un algoritm iterativ.
Am început cu b = 0, următoarea valoare va fi b_1 = b_0 – η*∂E/∂b, unde η este rata de învățare (hiper-parametru) și -η*∂E/∂b este dimensiunea pasului. Vom opri procesul de învățare atunci când dimensiunea pasului atinge pragul definit, în practică 0.001 sau mai mic. Pentru η = 0.3, b_1 = 0.48, b_2 = 0.528, b_3 = 0.5328 și b_4 = 0.53328 și b_5 = 0.5533328. După 5 iterații pasul a scăzut la 4.8e-5 și am oprit procesul de învățare aici. Valoarea lui b, obținută prin acest agloritm, este practic același ca valoarea obținută rezolvând ecuația ∂E/∂b=0.
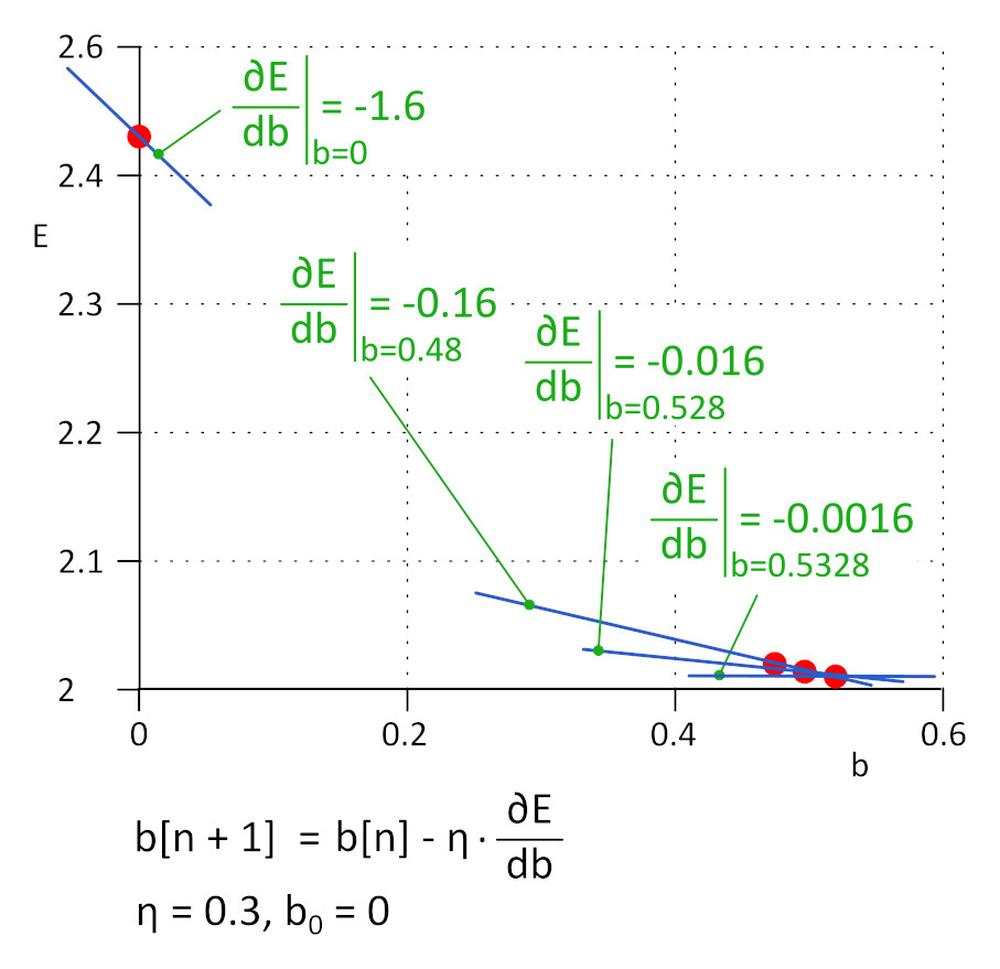
Această metodă este denumită gradient de coborâre.
Rata de învățare reprezintă un hiper-parametru important. Dacă este prea mică, necesită mulți pași pentru a găsi funcția de pierdere minimă; dacă este prea mare, algoritmul poate eșua. În practică, se folosesc variantele de algoritm îmbunătățite, cum ar fi Adam.
7.Repetăm pașii 5 și 6 până când valoarea funcției de pierdere descrește până la valoarea necesară.
8. Trecem setul de validare prin DNN-ul instruit și evaluăm precizia.
În acest moment, învățarea DNN este o muncă extrem de experimentală. Sunt cunoscute multe arhitecturi DNN, fiecare dintre ele fiind perfect adecvată pentru o plajă anume de sarcini. Fiecare arhitectură DNN are propriul set de hiper-parametri care influențează comportamentul DNN. Înarmați-vă cu răbdare iar rezultatele nu vor întârzia să apară.
Pentru mai multe informații privind produsele AAEON, vă rugăm nu ezitați să ne contactați la aaeon@soselectronic.com
Vă plac articolele noastre? Dacă da, atunci nu ratați nici unul! Nu trebuie să vă faceți griji în privința modului de livrare. Ne vom ocupa noi de tot pentru dvs.




