Sztuczna inteligencja na brzegu Twojej sieci

Dlaczego teraz?

W ramach obecnego stanu technologii można nauczyć głęboką sieć neuronową (DNN) wykonywać konkretne zadania, takie jak wykrywanie i rozpoznawanie obiektów i twarzy, rozpoznawanie mowy, tłumaczenie języków, granie w gry (szachy, go itp.), autonomiczne prowadzenie pojazdów, monitorowanie stanu czujników oraz predykcyjne podejmowanie decyzji dotyczących konserwacji maszyn, ocena rentgenogramów w służbie zdrowia itp. W przypadku takich wyspecjalizowanych zadań DNN może dorównać ludzkim możliwościom, a nawet je przewyższyć.

Dlaczego warto zastosować sztuczną inteligencję na brzegu sieci

W nowoczesnych budynkach na przykład znajduje się mnóstwo czujników, urządzeń grzewczych, wentylacyjnych i klimatyzacyjnych, wind, kamer monitoringu itp. podłączonych do sieci wewnętrznej. Ze względów związanych z bezpieczeństwem, czasem oczekiwania lub odpornością lepiej jest realizować zadania związane ze sztuczną inteligencją na miejscu, na brzegu sieci lokalnej, i przesyłać do chmury wyłącznie zanonimizowane dane niezbędne do podejmowania decyzji na szczeblu globalnym.

Sprzęt na brzegu sieci

Do wdrożenia DNN na brzegu potrzebne jest urządzenie charakteryzujące się jednocześnie wystarczająco dużą mocą obliczeniową oraz niskim zużyciem energii. Obecny stan technologii oferuje możliwość skorzystania z połączenia cechującego się niskim poziomem zużycia energii procesora głównego CPU oraz akceleratora VPU (komputer jednopłytkowy (SBC) z procesorem x86 + akcelerator VPU Intel Myriad X ) lub procesora głównego CPU i akceleratora graficznego GPU (CPU z architekturą ARM + GPU firmy Nvidia).

Najłatwiejszym sposobem rozpoczęcia stosowania DNN jest wykorzystanie zestawu deweloperskiego UP Squared AI Vision X Developer Kit w wersji B. Opiera się on na komputerze jednopłytkowym UP Square wyposażonym w procesor Intel Atom®X7-E3950 oraz 8GB pamięci RAM, 64 GB pamięci eMMC, moduł AI Core X z procesorem VPU Myriad X MA2485 i kamerę USB o rozdzielczości 1920 x 1080, z ręcznym ustawianiem ostrości. Zestaw dostarczany jest z preinstalowanym systemem Ubuntu 16.04 (jądro 4.15) oraz zestawem narzędzi OpenVINO 2018 R5.

Zestaw narzędzi zawiera prekompilowane aplikacje demonstracyjne w folderze /home/upsquared/build/intel64/Release oraz poddane wstępnemu uczeniu modele w folderze /opt/intel/computer_vision_sdk/deployment_tools/intel_models. Aby zapoznać się z pomocą dla dowolnej spośród aplikacji demonstracyjnych należy uruchomić ją w terminalu z opcją –h. Zaleca się dokonać inicjalizacji środowiska OpenVINO przed uruchomieniem aplikacji demonstracyjnej korzystając z polecenia source /opt/intel/computer_vision_sdk/bin/setupvars.sh.

Oprócz zestawu UP Squared AI Vision X Developer Kit, AAEON oferuje również:

1.Moduły bazujące na VPU Myriad X MA2485: AI Core X (pełnowymiarowa karta mPCIe, 1x Myriad X), AI Core XM 2280 (klucz B+M M.2 2280, 2x Myriad X), AI Core XP4/ XP8 (karta PCIE [x4], 4 lub 8x Myriad X).
2.Serię BOXER-8000 bazującą na module Nvidia Jetson TX2.
3.BOXER-8320AI z procesorem Core i3-6100U lub Celeron 3955U oraz 2 pełnowymiarowymi gniazdami mPCIe na moduły AI Core X.
4.Serię Boxer-6841M z płytą główną dla 6 / 7 generacji procesora Intel Core-I lub Xeon współpracującego z gniazdem LGA1151 oraz 1 gniazdem PCIe [x16] lub 2 gniazdami PCIe [x8] dla GPU o maksymalnym zużyciu energii wynoszącym 250W.

Sprzęt do nauki

W tabeli poniżej przedstawiono podsumowanie informacji dotyczących teoretycznej wydajności szczytowej sprzętu.

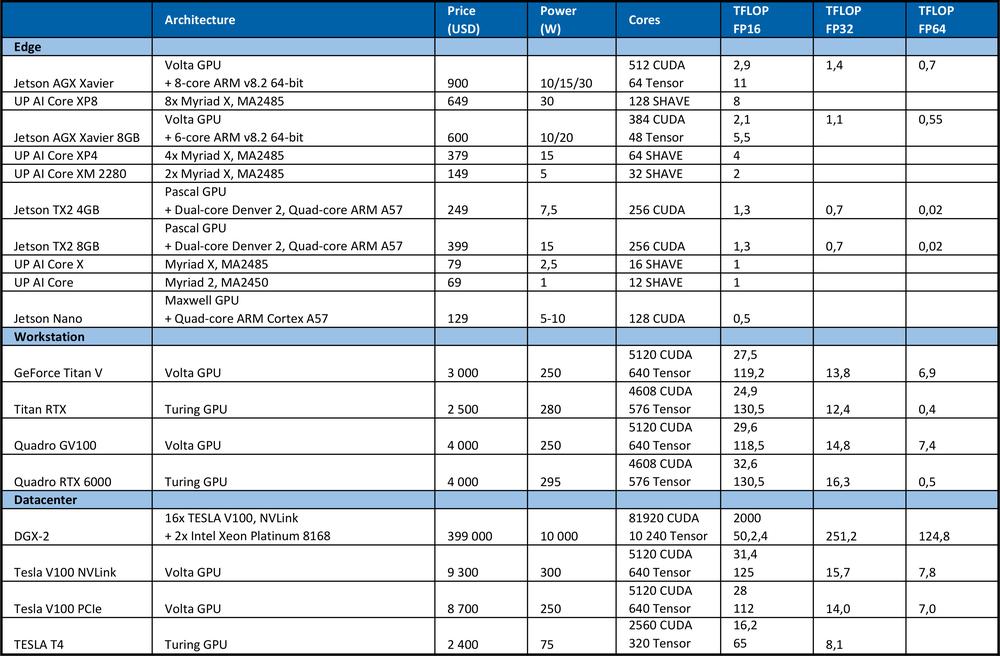
Dla porównania, należący do segmentu high end procesor Intel Xeon Platinum 8180
●wyposażony jest w 28 rdzeni z 2 jednostkami AVX-512 FMA na rdzeń
●charakteryzuje się częstotliwością turbo AVX-512 wynoszącą 2,3GHz w przypadku aktywności wszystkich rdzeni
●kosztuje 10,000 USD.

Oferowana teoretyczna wydajność szczytowa: liczba rdzeni * częstotliwość w GHz * AVX-512 DP FLOPS/Hz * liczba jednostek AVX-512 * 2 = 2060,8 GFLOPS w przypadku klasy podwójnej precyzji (DP) → 4,1216 TFLOPS w przypadku klasy pojedynczej precyzji (32 bity).

Jak widać w tabeli powyżej, procesor GPU zapewnia o wiele większą wydajność na potrzeby uczenia sieci neuronowych. Należy pamiętać, że liczba operacji na sekundę to nie jedyny parametr wpływający na wydajność uczenia. Czynniki takie jak wielkość pamięci RAM, szybkość przesyłu danych pomiędzy procesorem głównym a pamięcią RAM, procesorem graficznym i pamięcią RAM procesora graficznego oraz pomiędzy procesorami graficznymi także wpływają na prędkość uczenia.

Oprogramowanie

OpenVINO
Zestaw narzędzi OpenVINO (open visual inference and neural network) to darmowe oprogramowanie umożliwiające szybkie wdrażanie aplikacji i rozwiązań emulujących ludzki wzrok.

Zestaw narzędzi OpenVINO:
●wykorzystuje CNN (konwolucyjną sieć neuronową)
●może dzielić obliczenia pomiędzy procesorem głównym firmy Intel, zintegrowanym procesorem graficznym, układem Intel FPGA, kluczem Intel Movidius Neural Compute Stick oraz akceleratorami wizyjnymi z procesorami VPU Intel Movidius Myriad
●zapewnia zoptymalizowany interfejs do współpracy z bibliotekami OpenCV, OpenCL oraz OpenVX
●obsługuje frameworki Caffe, TensorFlow, MXNet, ONNX oraz Kaldi

TensorFlow
TensorFlow to biblioteka typu open source do obliczeń numerycznych i uczenia maszynowego. Oferuje ona wygodny w użyciu, fasadowy (front-end) interfejs API do tworzenia aplikacji w języku programowania Python. Aplikacje stworzone przy użyciu TensorFlow konwertowane są na zoptymalizowany kod C++, mogący działać na szeregu platform, takich jak procesory główne, procesory graficzne, komputery lokalne, klaster w chmurze, osadzone urządzenia na brzegu sieci itp.

Inne użyteczne oprogramowanie
Jupyter Lab / Notebook
https://jupyter.org/index.html
https://github.com/jupyter/jupyter/wiki/Jupyter-kernels
https://jupyterlab.readthedocs.io/en/stable
Keras
Pandas 
MatplotLib 
Numpy 

Jak to działa

Uproszczony model neuronu
Uproszczony model neuronu - budulec sieci perceptron - został po raz pierwszy opisany przez Warrena McCullocha oraz Waltera Pittsa w roku 1943 i nadal stanowi standard referencyjny w obszarze sieci neuronowych.

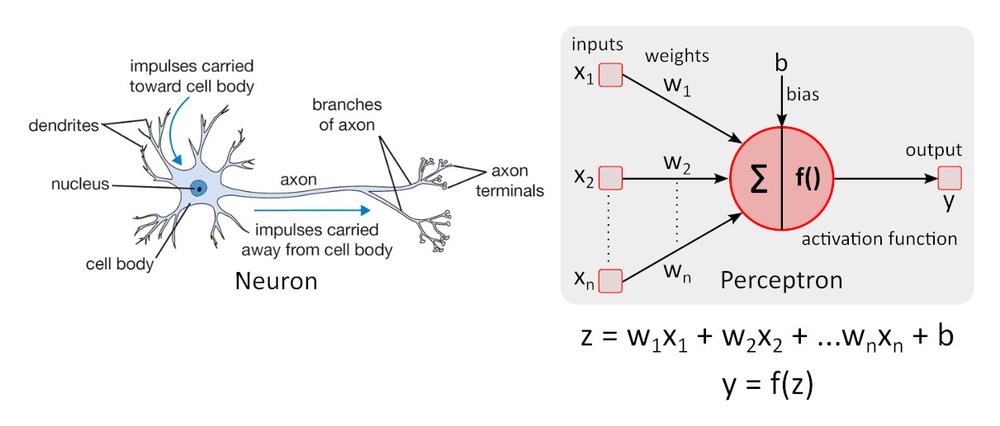
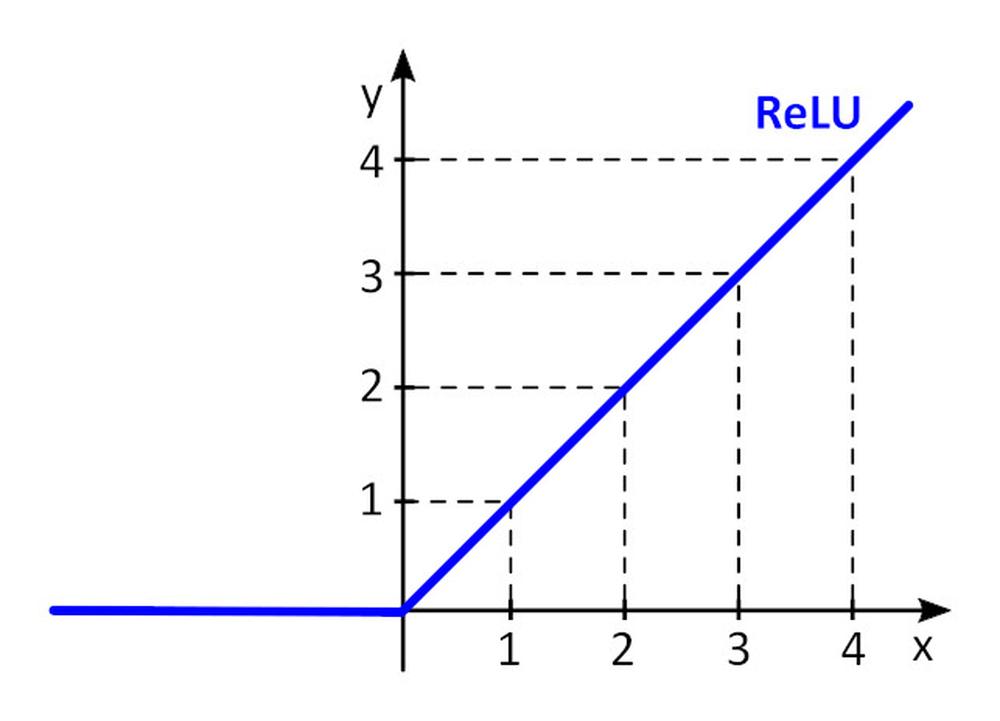
Funkcja aktywacji f () uzupełnia perceptron o nieliniowość. Bez nieliniowej funkcji aktywacji w sieci neuronowej (SN) składającej się z perceptronów, niezależnie od liczby warstw sieć ta zachowywałaby się tak jak perceptron jednowarstwowy, gdyż zsumowanie warstw dawałoby jedynie kolejną funkcję liniową. Najczęściej wykorzystywaną funkcją aktywacji jest tzw. rektyfikowana jednostka liniowa (ang. rectified linear unit, ReLU).

y = f(x) = maks. (0, x), dla x < = 0, y = 0, dla x ≥ 0, y=x

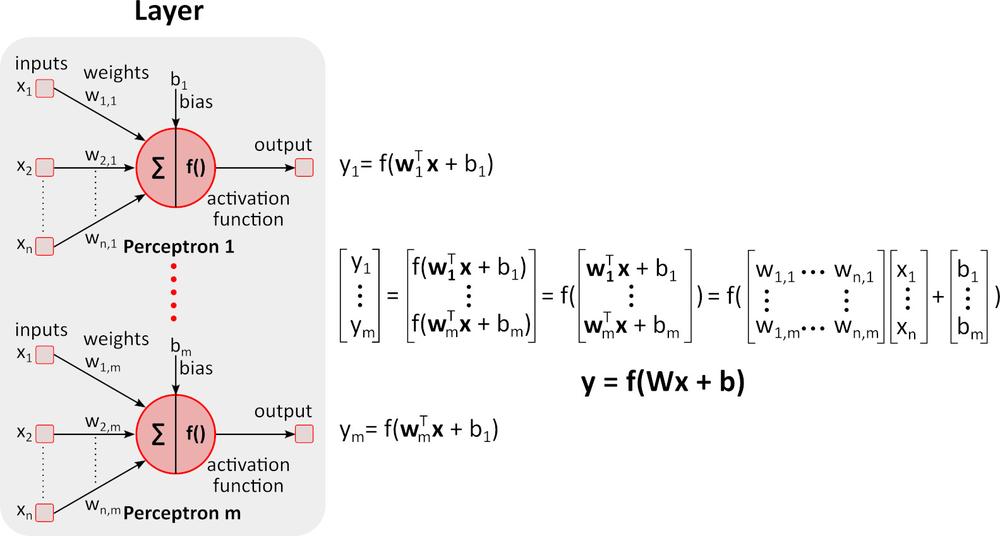
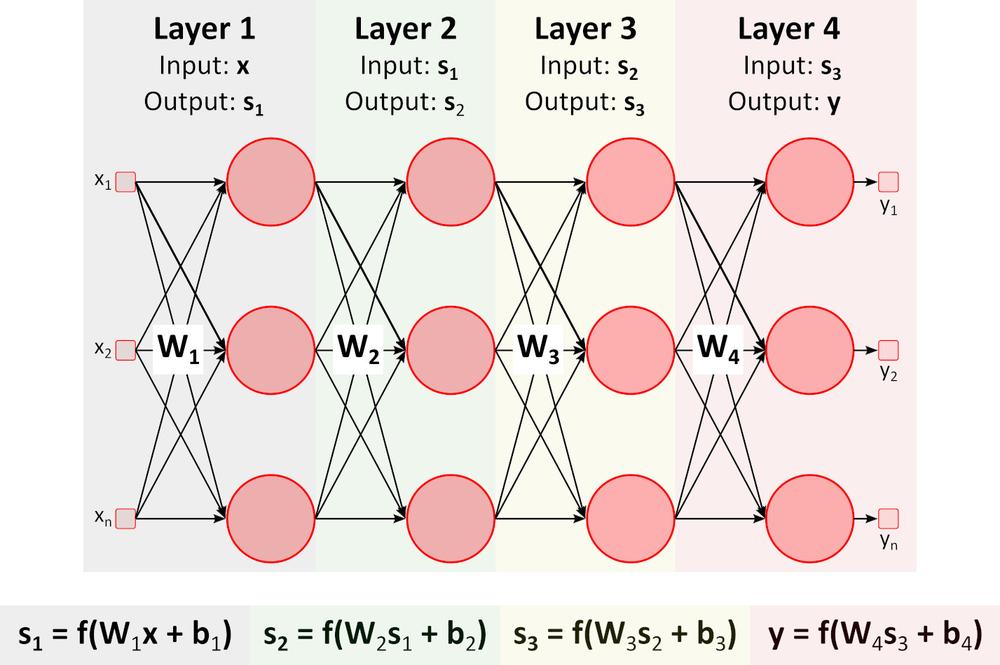
Wnioskowanie (przejście w przód (ang. forward pass))

Na rysunku powyżej widnieje głęboka sieć neuronowa (DNN). Wynika to z faktu, że pomiędzy warstwami wejścia i wyjścia zawiera liczne inne warstwy. Jak można zauważyć, DNN wymaga mnożenia i dodawania macierzy. Specjalistyczny sprzęt zoptymalizowany do tego typu zadań, taki jak procesor graficzny GPU (graphics processing unit) czy procesor wizyjny VPU (vision processing unit) działa znacznie szybciej niż układ CPU (jednostka centralna, procesor) przeznaczony do zadań ogólnych, a także charakteryzuje się niższym zużyciem energii.

Uczenie (przejście wstecz (ang. backward pass))

Powiedzmy, że chcemy nauczyć sieć DNN rozpoznawać pomarańcze, banany, jabłka oraz maliny (klasy obiektów) widoczne na obrazie.

1. Przygotowujemy dużą liczbę obrazów owoców wymienionych powyżej i dzielimy je na zbiory treningowy oraz walidacyjny. Zbiór treningowy zawiera obrazy i prawidłowe, wymagane wyjścia dla tych obrazów. DNN będzie miała 4 wyjścia. Na pierwszym wyjściu otrzymujemy wynik (prawdopodobieństwo) określający, że owoc widoczny na obrazie to pomarańcza, na drugim wynik określający, że ten owoc to banan itd.

2.Ustawiamy wartości początkowe wszystkich wag w_i oraz wyrazów wolnych (bias) b_i. Zazwyczaj stosuje się wartości losowe.

3.Wprowadzamy do DNN pierwszy obraz. Na każdym wyjściu otrzymujemy wynik (prawdopodobieństwo). Powiedzmy, że pierwszy obraz przedstawia pomarańczę. Wartości na wyjściach sieci mogą przedstawiać się następująco y= (pomarańcza, banan, jabłko, malina) = (0,5, 0,1, 0,3, 0,1). Sieć „mówi”, że sygnałem wejściowym jest pomarańcza, z prawdopodobieństwem wynoszącym 0,5.

4.Definiujemy funkcję straty (błędu) określającą ilościowo zgodność przewidywanych wyników i prawidłowych wyników dla każdej klasy. Często stosuje się funkcję E = 0,5*suma (e_j) ^2, gdzie e_j = y_j - y_rzeczywiste_j, zaś j to liczba obrazów w zbiorze treningowym. E_1_pomarańcza = 0,5*(0,5-1)^2=0,125, E_1_banan =.0,5*(0,1-0)^2 = 0,005 E_1_jabłko = 0,5*(0,3-0)^2 = 0,045, E_1_malina = 0,5*(0,1-0)^2 = 0,005 E_1 = (0,125, 0,005, 0,045, 0,005)

5.Wprowadzamy wszystkie pozostałe obrazy ze zbioru treningowego do sieci DNN i obliczamy wartość funkcji straty E (E_pomarańcza, E_banan, E_jabłko, E_malina) dla całego zbioru treningowego.

6.W celu zmodyfikowania wszystkich wag w_i i wyrazów wolnych b_i dla kolejnego przebiegu treningowego (epoki) musimy znać wpływ każdego parametru w_i oraz b_i na funkcję straty dla każdej klasy. Jeśli zwiększenie wartości parametru powoduje zwiększenie wartości funkcji straty, należy ten parametr obniżyć i na odwrót. Ale jak wyliczyć wymaganą wartość zwiększenia lub zmniejszenia parametrów?

Spójrzmy na prosty przykład.

Mamy trzy punkty o współrzędnych (x, y): (1, 3), (2,5, 2), (3,5, 5). Chcemy znaleźć linię y = w.x + b dla której wartość funkcji straty E = 0,5*suma (e_j) ^2 , gdzie e_j = y_j – y_rzeczywiste_j, j=1, 2, 3, jest minimalna. Aby jak najbardziej uprościć to zadanie, przyjmijmy, że w=1,2 i potrzebujemy ustalić optymalną wartość wyłącznie dla b. Przybieramy wartość początkową dla b=0.

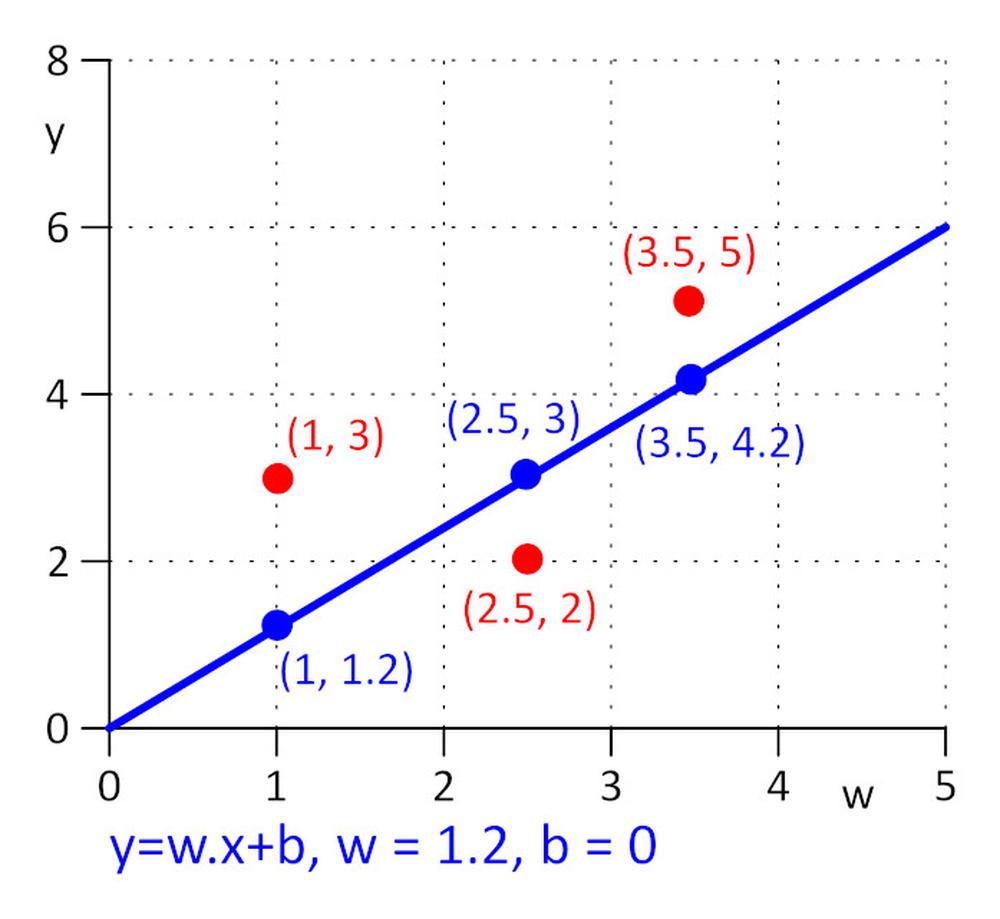
Obliczmy wartość funkcji straty: E = 0,5*suma (e_j) ^2 = 0,5*(e_1^2 + e_2^2 + e_3^2), e_1=1,2*1 + b -3, e_2 = 1,2*2,5 + b – 2, e_3 = 1,2*3,5 + b – 5.

Funkcja straty E jest prosta, możemy znaleźć minimalną wartość E rozwiązując równanie: ∂E/∂b = 0. Jest to funkcja złożona, w celu obliczenia ∂E/∂b stosujemy wzór na pochodną funkcji złożonej.

∂E/∂b=0.5*((∂E/∂e_1)*(∂e_1/∂b) + (∂E/∂e_2)*(∂e_2/∂b) + (∂E/∂e_3)*(∂e_3/∂b)) = 0.5*(2*e_1*1 + 2*e_2*1 + 2*e_3*1) = (1.2*1 + b – 3) + (1.2*2.5 + b – 2) + (1.2*3.5 + b – 5) = 0 => b = 0.53333.

W praktyce liczba parametrów w_i i b_i może wynosić milion lub więcej, zatem bezpośrednie rozwiązywanie równania ∂E/∂b_i = 0 oraz ∂E/∂b_i = 0 jest niepraktyczne. Należy zastosować algorytm iteracyjny.

Rozpoczęliśmy od b = 0, kolejną wartością będzie b_1 = b_0 – η*∂E/∂b, gdzie η to szybkość uczenia (hiperparametr) a -η*∂E/∂b to wielkość kroku. Kończymy uczenie gdy wielkość kroku osiągnie określony próg, w praktyce 0,001 lub mniej.

Dla η = 0,3, b_1 = 0,48, b_2 = 0,528, b_3 = 0,5328 oraz b_4 = 0,53328 i b_5 = 0,5533328. Po 5 iteracjach wielkość kroku spadła do 4,8e-5 i w tym miejscu kończymy uczenie. Wartość b otrzymana przy użyciu tego algorytmu jest praktycznie taka sama jak wartość otrzymana poprzez rozwiązanie równania ∂E/∂b=0.

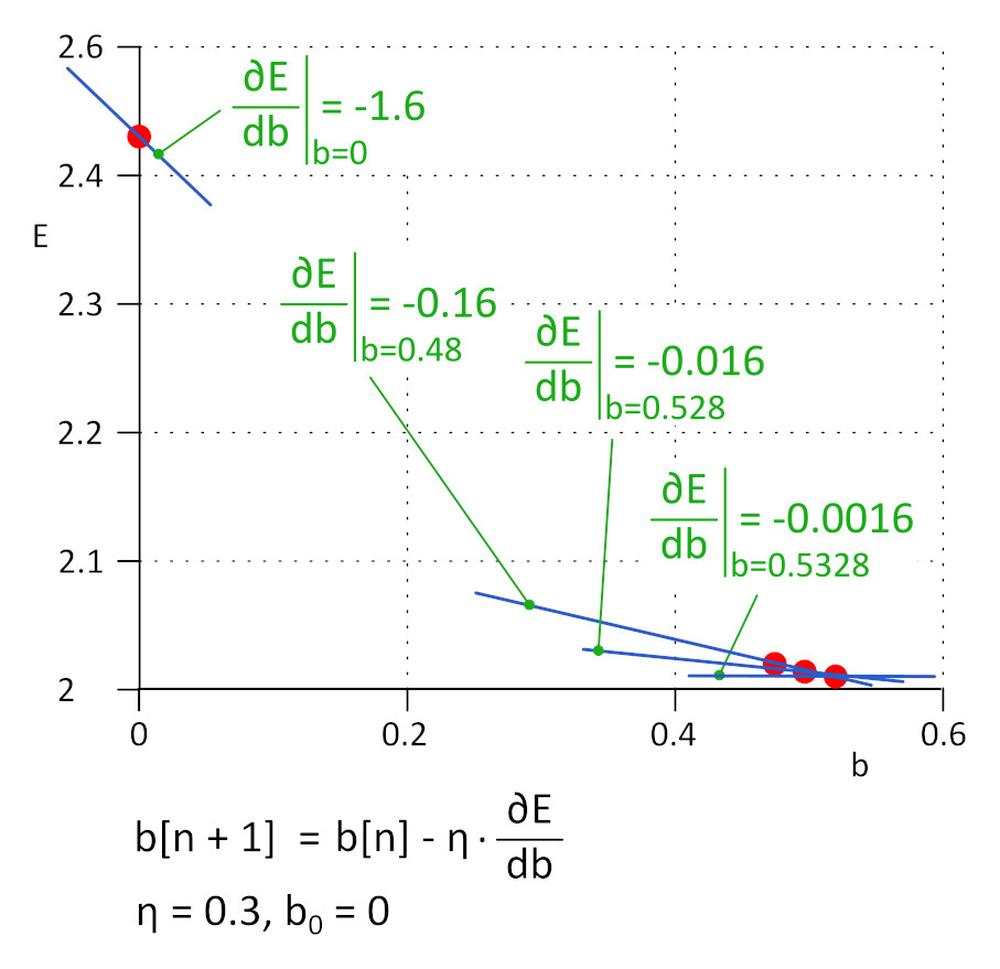
Metoda ta nazywana jest metodą spadku gradientu (gradient descent).

Szybkość uczenia to istotny hiperparametr. Jeśli jego wartość jest zbyt niska, znalezienie minimum funkcji straty odbywa się w zbyt wielu krokach. Jeśli jest zbyt wysoka, algorytm może zawieść. W praktyce stosuje się udoskonalone warianty algorytmu, takie jak Adam.

7.Powtarzamy kroki 5 i 6 do momentu, gdy wartość funkcji straty spadnie do wymaganej wielkości.

8.Do „nauczonej” sieci DNN wprowadzamy zbiór walidacyjny i oceniamy dokładność działania.

Obecnie uczenie sieci DNN ma charakter wysoce eksperymentalny. Znana jest duża liczba różnych odmian architektury DNN, przy czym każda z nich dopasowana jest do określonej grupy zadań. Każda architektura sieci DNN posiada własny zestaw hiperparametrów wpływających na zachowanie DNN. Uzbrój się w cierpliwość, a wyniki wkrótce się pojawią.

Aby otrzymać więcej informacji na temat produktów firmy AAEON, prosimy wysłać wiadomość na adres aaeon@soselectronic.com