(Prof. Ing. Dušan Levický, CSc., is professor at the Department of Electronics and Multimedia Telecommunications of the Technical University in Košice )
Cryptography has evolved from the times of Julius Ceasar (Ceasar's cipher) to various breakthrough ciphers in the Middle Ages and to mechanical ciphers, such as Enigma. Modern cryptography is stimulated mainly by the development of mathematics, information theory and the development of information and communication technologies.
It has become a modern science with a practical impact on privacy protection, security of electronic systems and security of electronic communications. Significant applications of cryptography are information and network security, e-mail, digital television, e-commerce, banking, and e-learning.
The message transfer in the earliest times brought the need to build secure communication that would allow the confidentiality of the message, or the communication itself. For this reason, methods of secret communication, steganography and cryptography, have been developed.
Steganography uses methods of concealing the communication by concealing the message in a way that a secret message transmission happens in the background of open communication.
Cryptography does not have the goal of concealing the existence of a secret message, or to conceal the communication. Its purpose is to conceal the content of the message using the encryption methods.
What Is Encryption
The process of editing a message that conceals its content is called encryption. Message being sent, which usually has the form of a text, is called plaintext. The result of the encryption is the encrypted message, or ciphertext. Encryption is thus the process of converting the plaintext into ciphertext. Decryption, deciphering is the process of obtaining the plaintext from the received ciphertext. The technique of encrypting the content of secret information is called cryptography. Systems, or encryption means are called cryptographic systems or simply ciphers. The technique of deciphering the ciphertext to obtain the plaintext is called cryptanalysis. An area that includes cryptography and cryptanalysis is called cryptology.
The Principle of Conventional Encryption
Classical or conventional cryptographic systems use the same secret key, both for encryption and decryption; therefore they are also referred to as cryptographic systems with secret key. Encryption in these cryptographic systems is referred to as symmetric encryption or single key encryption.
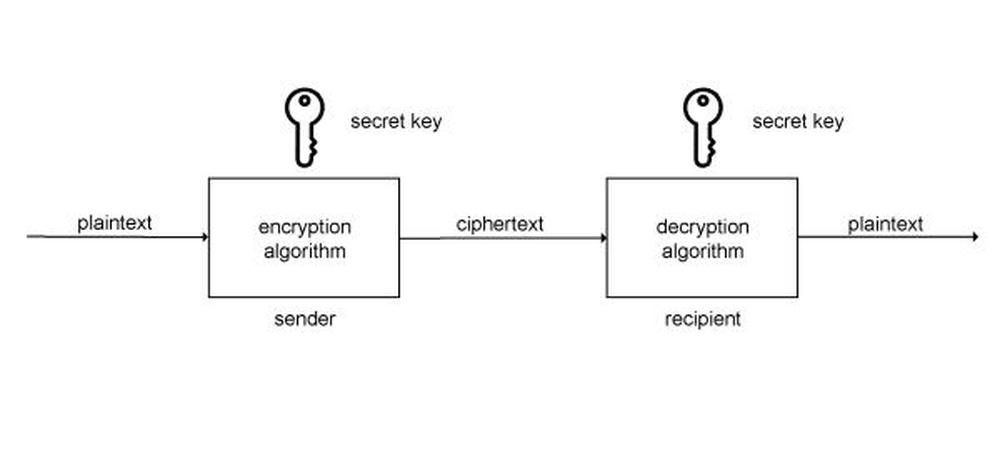
The principle of conventional encryption is illustrated in picture gallery.
Symmetric encryption includes five elements:
1. Plaintext is a message, or data that represents the input of the cryptographic system. These are the input data for the encryption algorithm.
2. Encryption algorithm is the algorithm that implements encryption, i.e. it transforms the plaintext into ciphertext using cryptographic techniques, e.g. substitution and permutation.
3. Secret key is also the input of the cryptographic system and it does not depend on the plaintext. A secret key specifies the particular shape of the plaintext transformation to ciphertext.
4. Ciphertext represents the output of the encryption algorithm. It is univocally set by the plaintext and a secret key. For the given plaintext, two different secret keys produce two different ciphertexts.
5. Decryption algorithm realizes the process of obtaining the plaintext from the received ciphertext using the same secret key that was used for encryption.
Since the cryptographic algorithms cannot be successfully conceived for a long time, the security of conventional encryption is built exclusively on key secrecy.
Cryptography systems and their operations
Cryptographic systems or encryption algorithms use two basic types of operations:
Substitution that replaces any plaintext element (bit, letter, group of bits and letters) with other plaintext elements and these new elements remain in the place of the original elements. The recipient must use an inverse substitution to obtain the plaintext.
Transposition as rearranging plaintext elements as per certain rule, e.g. permutation. The recipient must use inverse transposition to obtain the plaintext. Simply put, we can talk about substitution and transposition ciphers.
The basic requirement for cryptographic operations is that no information is lost when they are applied, i.e. they must be invertible.
In terms of the number and types of keys, cryptographic systems can be divided into cryptographic systems with secret key and cryptographic systems with public key
Cryptographic systems with secret key
These systems use the same encryption and decryption keys and are also referred to as symmetrical or conventional cryptographic systems. The security of these systems lies in the confidentiality of the key that the sender and the recipient must exchange before the communication itself, which is a certain disadvantage in terms of communication readiness.
Cryptographic systems with public key
These systems use a different encryption key and decryption key, thus they use public and private key. The encryption key is so-called public key; the decryption key is a private key and is known only to the recipient.
Cryptographic systems with public key are also referred to as asymmetrical cryptographic systems and their security is based on the mathematical complexity of identifying a private key from a known public key.
Based on the plaintext processing method, cryptographic algorithms can use two basic types of modes:
1. Block mode is the basis of blockciphers that process block of the text at a time. Output is a block of ciphertext that usually has the same size as a block of plaintext.
2. Stream mode is the basis of stream ciphers that process the plaintext by taking one byte of the text at a time. Each element of the plaintext therefore corresponds to one element of ciphertext.
Algorithm Safety = Ability to Withstand Breakage
Absolutely safe cryptographic algorithm is characterized by the fact that cryptanalyst will not be able to get plaintext even when it has an unlimited amount of ciphertext and unlimited calculation capacity. This standpoint is only met by the one-timepad algorithm, which is not frequently used because of its practical use.
In practice, the security of cryptographic algorithms is usually judged according to how much effort is needed to break it. From the practical point of view, the cryptographic algorithm should fulfil the following conditions:
- costs needed to break the encryption algorithm is higher than the encrypted data value
- time needed to break the encryption algorithm is greater than the amount of time for which the encrypted data needs to be concealed.
These aspects take into account the so-called practical safety of cryptographic algorithms that can be characterized as computationally safe. These algorithms are considered strong if they cannot be broken by using current, or in the near future available, means for breakage.
Do you like our articles? Do not miss any of them! You do not have to worry about anything, we will arrange delivery to you.